Предмет: Алгебра,
автор: mashunka09
Вычислить интеграл.
Приложения:
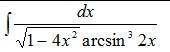
Ответы
Автор ответа:
0
Замена переменной:
Автор ответа:
0
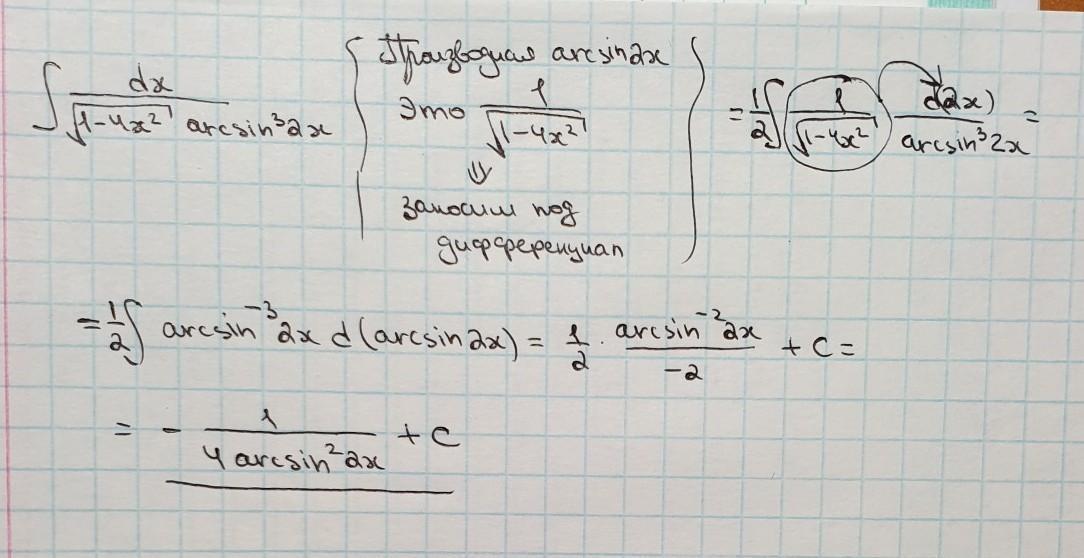
Ответ:
решение на фотографии
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Evelina1
Предмет: Русский язык,
автор: Лерочка1996
Предмет: Русский язык,
автор: Анилора
Предмет: Математика,
автор: ChizuNyan
Предмет: Литература,
автор: alyosha2641