Предмет: Алгебра,
автор: PetrKalash
Дам 100 баллов за решение тригонометрического уравнения
Приложения:
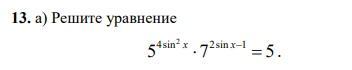
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Юлёк022001
Предмет: Английский язык,
автор: asd371738
Предмет: Русский язык,
автор: meln888
Предмет: Математика,
автор: svepielisz
Предмет: История,
автор: Macdaddy1146