Предмет: Алгебра,
автор: brivach76
2cos^2(2x)-√3sin4x+sin2x-√3cos2x-5=0
Приложения:
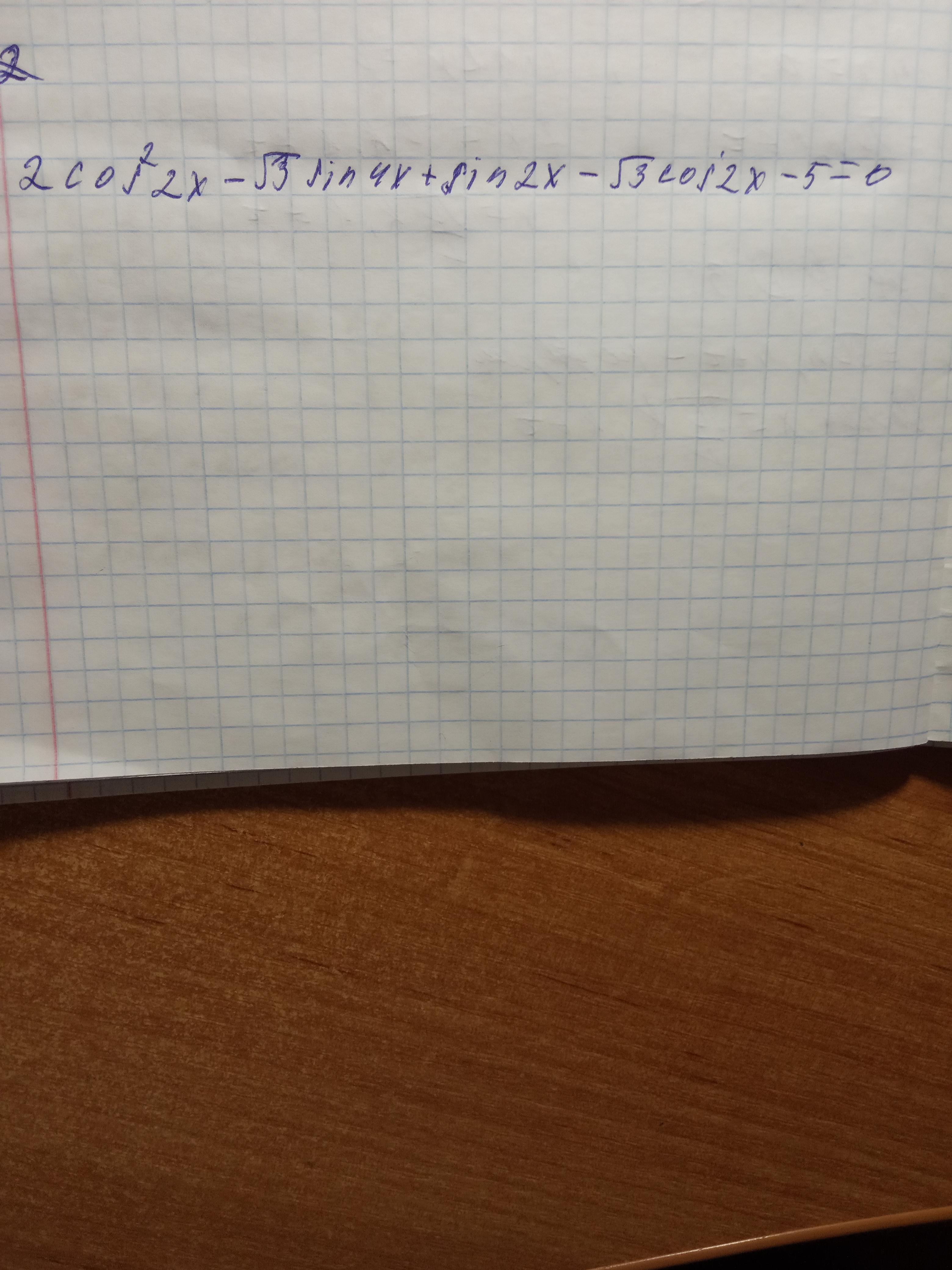
Ответы
Автор ответа:
0
так как
и
то
или
Применяем метод вспомогательного угла
Делим каждое уравнение на 2:
или
или
так как |sint|≤1 первое уравнение не имеет решений
это о т в е т.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська література,
автор: filich
Предмет: Українська література,
автор: анжела14
Предмет: Алгебра,
автор: помогите851
Предмет: Математика,
автор: adelina2004UFA