Предмет: Математика,
автор: Svika98
Вычислить предел (не по правилу Лопиталя)
Приложения:
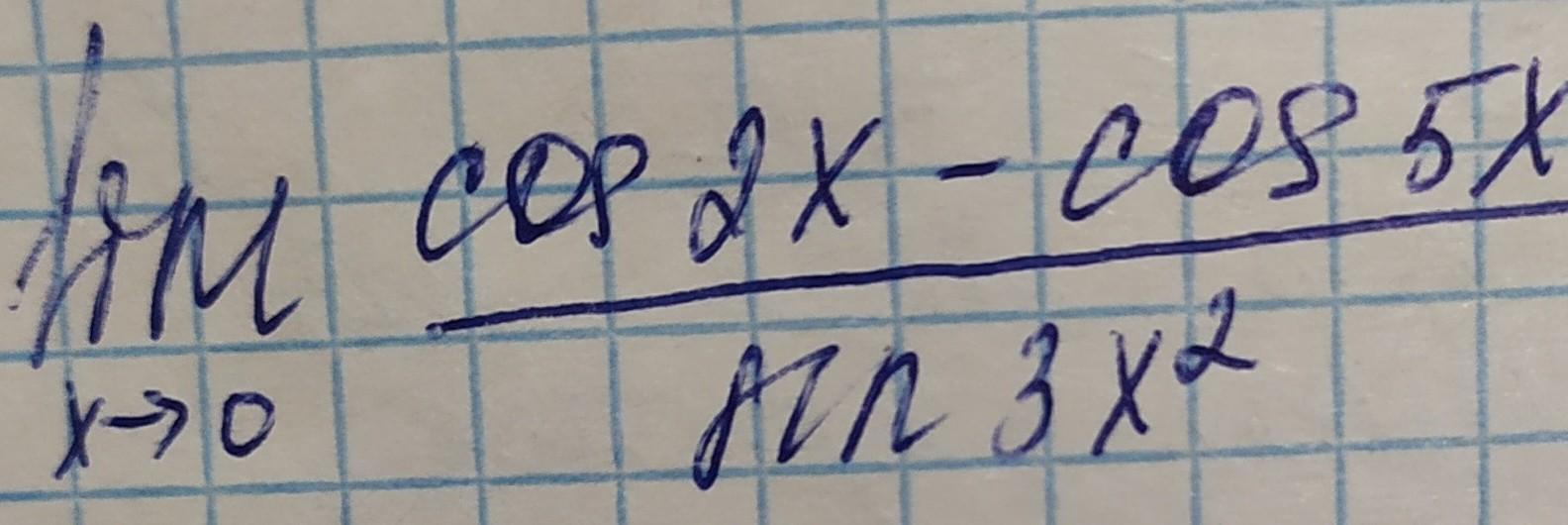
Ответы
Автор ответа:
0
Домножим числитель и знаменатель на :
Теперь запишем наш предел как произведение пределов (каждый из них, разумеется, существует): ; Первый из них - это первый замечательный предел. Имеем:
. Теперь запишем разность косинусов как произведение синусов:
; Теперь каждый из пределов-сомножителей можно подогнать к замечательному пределу:
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: гениальность
Предмет: Английский язык,
автор: Helena85
Предмет: Русский язык,
автор: ilyuza5
Предмет: Алгебра,
автор: Ch100alo