Предмет: Математика,
автор: HopiTakeo
Математический анализ. Найти интеграл
Приложения:
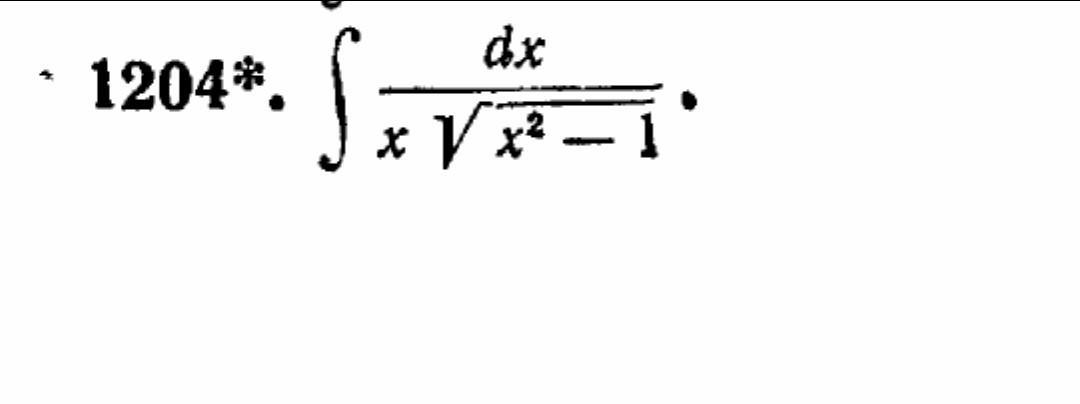
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: giiiiiiiiiiiiiiii
Предмет: Русский язык,
автор: maechik
Предмет: Русский язык,
автор: markcrav4enko
Предмет: Алгебра,
автор: darkseal
Предмет: Алгебра,
автор: nik1513