Предмет: Алгебра,
автор: ab29632131231
Найти интегрированием по частям ОТДАЮ ВСЕ БАЛЛЫ
Приложения:
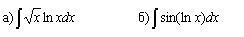
Ответы
Автор ответа:
1
ab29632131231:
Огромное Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: nikitinas
Предмет: Русский язык,
автор: Cat005
Предмет: Русский язык,
автор: Стегал
Предмет: Биология,
автор: maxik495
Предмет: Информатика,
автор: VaskasTV