Предмет: Алгебра,
автор: morisha
Значение тригонометрических функций , вычислите значения выражения
Приложения:
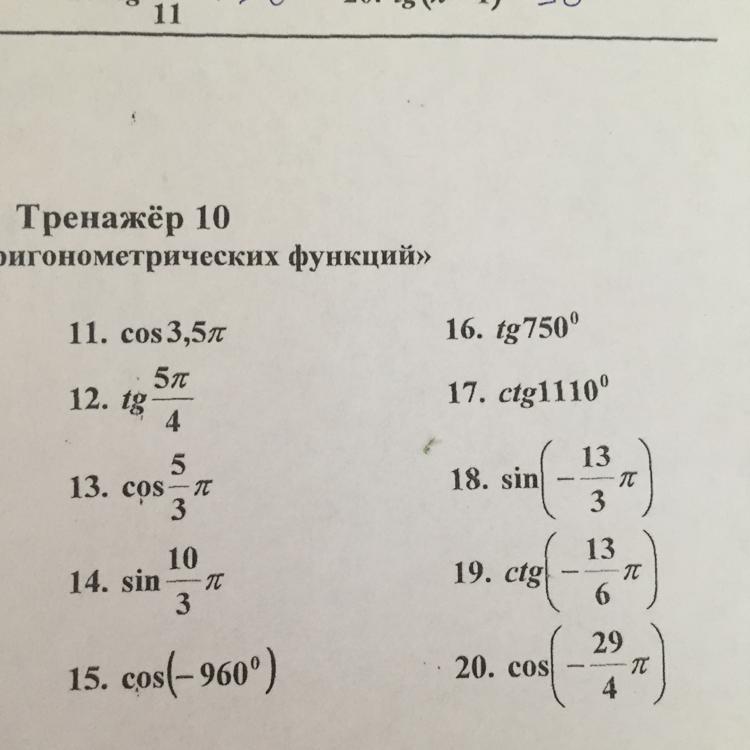
Ответы
Автор ответа:
4
Ответ:
11.cos(3,5p)=cos270°= 0
12.tg(5p/4)tg225°=tg(270°-45°)=ctg45°=1
13.cos(5p/3)=cos300°=cos(270°+30°)=sin30°=1/2
14.sin(10p/3)=sin600°=sin240°=sin(270°-30°)=-cos30°=-√3/2
15. cos(-960)=cos240°=cos(270-30)=-sin30=-1/2
16.tg750°=tg30°=√3/3
17.ctg1110°= ctg30°=√3
18.sin(-13p/3)=-sin60°=-√3/2
19.ctg(-13p/6)=ctg390°=-ctg30°=-√3
20.cos(-29p/4)=cos1305°=cos225°=cos(270°-45°)=-sin45°=-√2/2
MizoriesKun:
Где расчёты ???
Что тут считать
Ребёнок как не понимал ,так и не поймёт откуда ,что взялось ?)) это нам понятно.... ,а ему. ???
((
Есть два варианта ,расписать или удалить
Что делаем ??
Ок мне не трудно
Автор ответа:
3
Идеально ,только в одном примере остался корень в знаменателе
так это табличное значение)
Похожие вопросы
Предмет: Английский язык,
автор: DuckTheSystem
Предмет: Українська мова,
автор: красницкая
Предмет: Русский язык,
автор: irishka300868
Предмет: Биология,
автор: максим200726
Предмет: Химия,
автор: Jacksi