Предмет: Алгебра,
автор: rushikkkko
Народ, нужна помощь с примером, буду благодарен за ответ и поэтому даю 40 баллов.
Приложения:
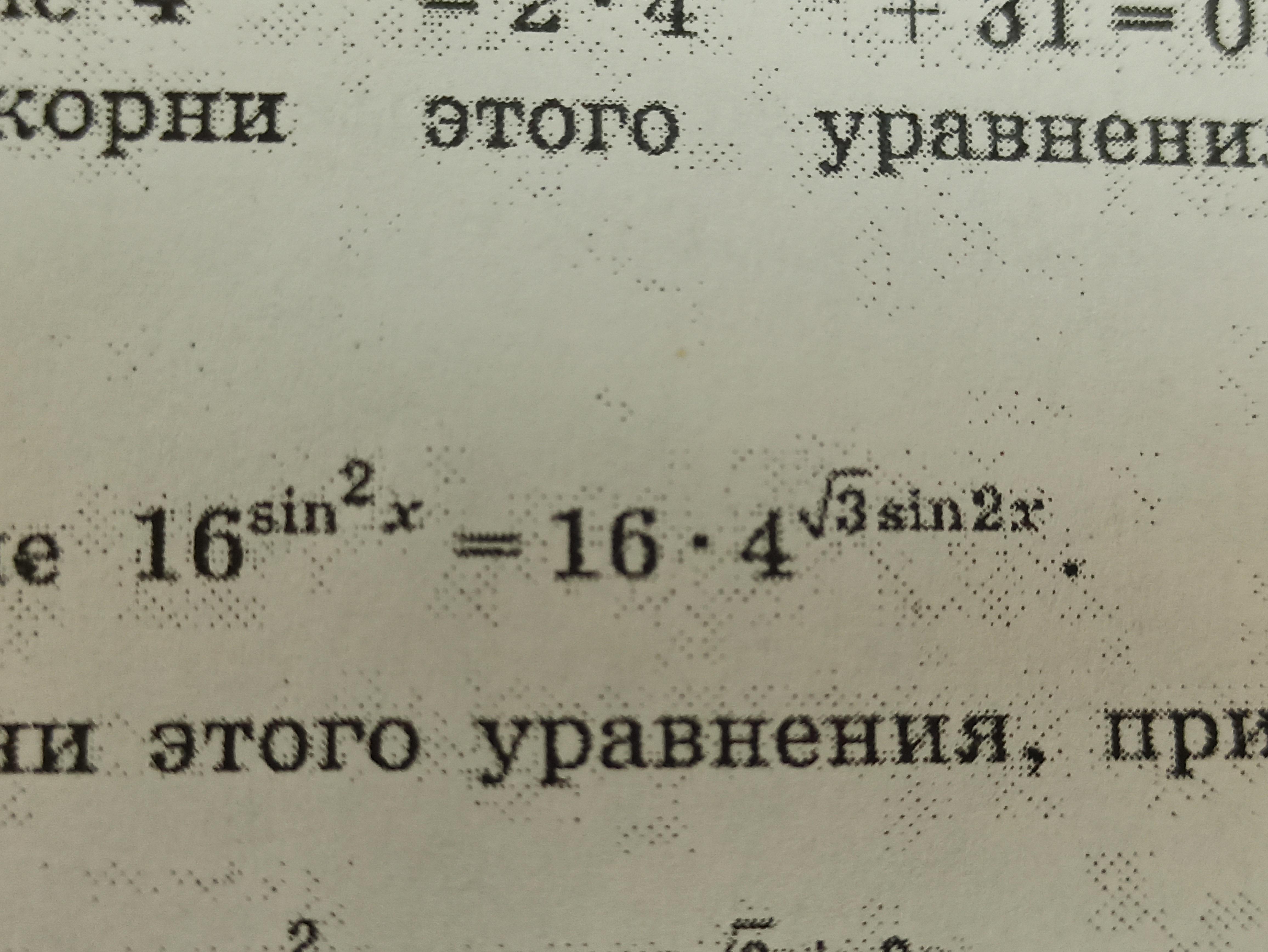
Ответы
Автор ответа:
0
Ответ:
Вроде бы, так
Объяснение:
Приложения:
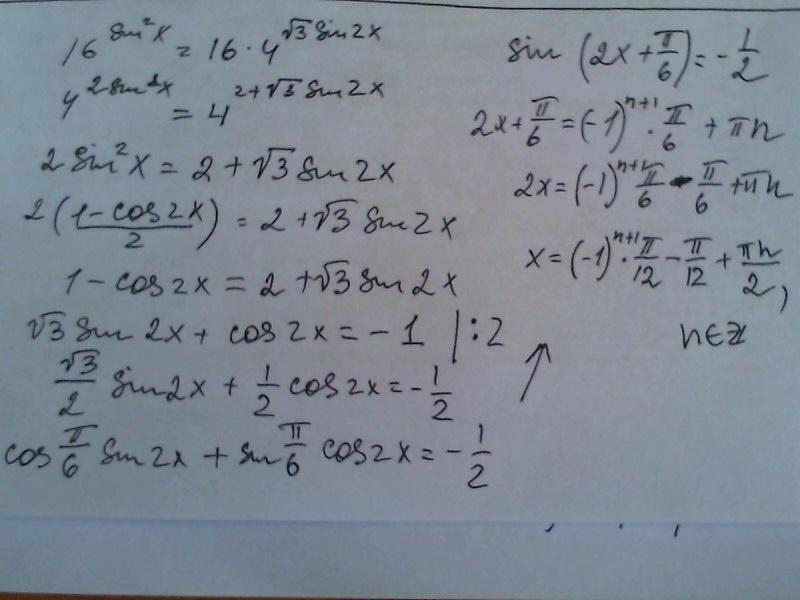
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: daryabugaeva
Предмет: Русский язык,
автор: ivankaban
Предмет: Английский язык,
автор: alexa2011
Предмет: Математика,
автор: Сирена27
Предмет: Музыка,
автор: Аноним