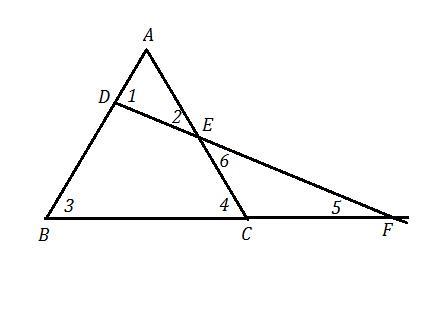
прямая пересекает две боковые стороны AB и AC равнобедренного треугольника ABC в точках D и Е соответственно, а луч BC в точке F. Докажите, что АЕ>AD. (рис. 3.22)

Ответы
ΔАВС - равнобедренный , АВ=АС ⇒ ∠В=∠АСВ .
Рассм. ΔADE. Чтобы доказать, что АЕ>AD , надо доказать, что ∠ADE>∠AED , так как против бОльшего угла лежит бОльшая сторона .
Рассм. ΔBDF. Внешний угол этого треугольника ∠ADF=∠ADE равен сумме двух углов треугольника, не смежных с ним, то есть
∠ADE=∠B+∠BFD , но ∠В=∠АСВ ⇒ ∠ADE=∠ACB+∠BFD .
Но ∠АСВ - это внешний угол ΔCEF , и поэтому ∠ACB=∠CEF+∠CFE .
Значит, ∠ADE=∠CEF+∠CFE+∠BFD .
Но ∠CFE - это тот же самый угол, что и ∠BFD , ∠CFE=∠BFD .
∠ADE=∠CEF+2*∠CFE
∠CEF=∠AED как вертикальные углы, поэтому
∠ADE=∠AED+2*∠CFE
То есть один ∠ADE равен одному ∠AED плюс ещё два угла ∠CFE , значит ∠ADE>∠AED и сторона, лежащая против ∠ADE (сторона АЕ) больше стороны, лежащей против ∠AED (сторона AD).
AE>AD
Или запись короче, если обозначить углы, как на рисунке:
∠1=∠3+∠5=∠4+∠5=(∠6+∠5)+∠5=∠6+2*∠5=∠2+2*∠5 ⇒
∠1=∠2+2*∠5 , ∠1 >∠2 ⇒ АЕ>AD .