Предмет: Геометрия,
автор: luntick14
ПОМОГИТЕ ПЖ
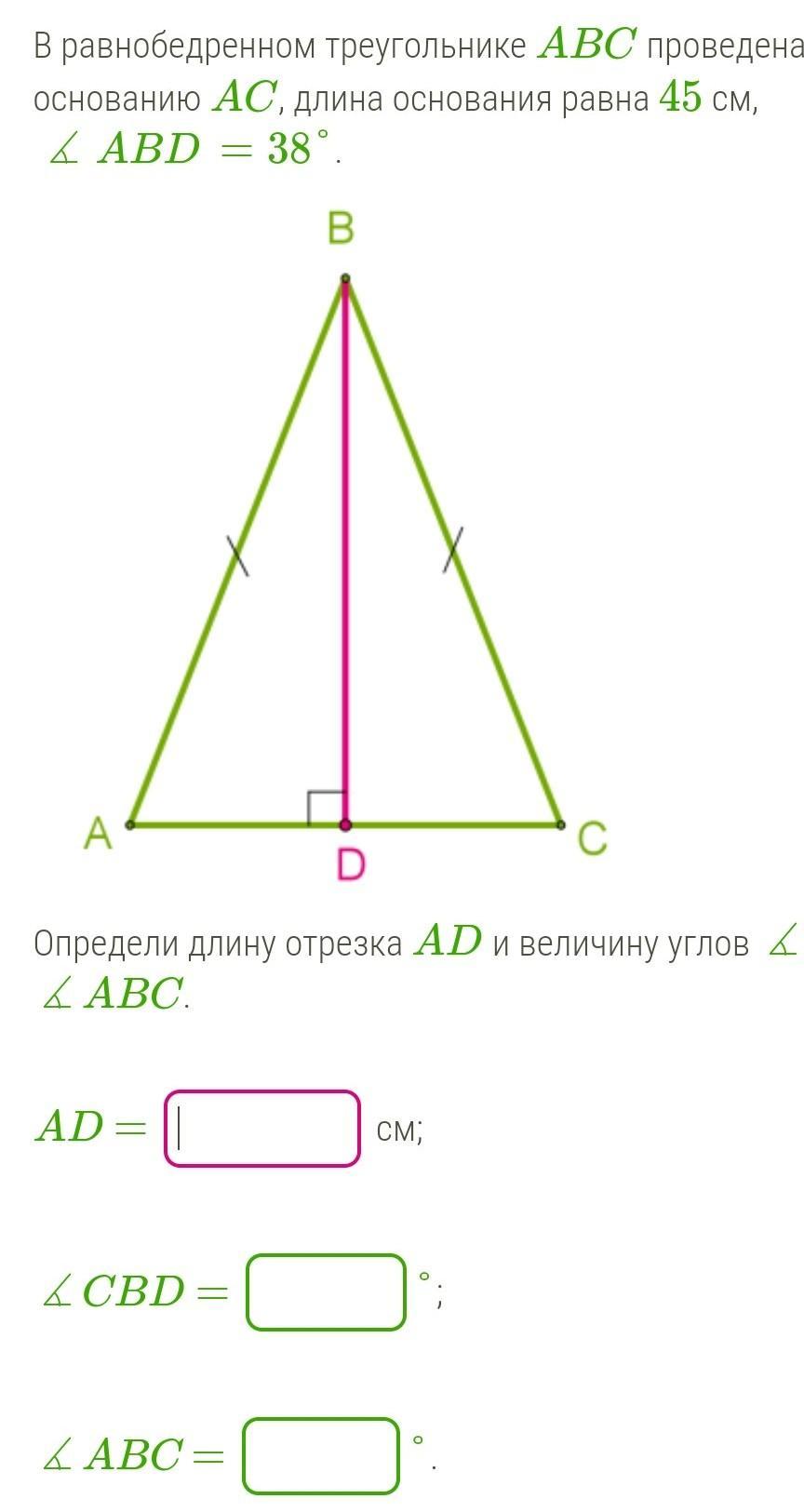
В равнобедренном треугольнике ABC проведена высота к основанию AC, длина основания равна 45 см, ∡ABD=38°.
Определи длину отрезка AD и величину углов ∡CBD и ∡ABC.
AD =
см;
∡CBD =
°;
∡ABC =
°.
Приложения:
Ответы
Автор ответа:
17
По свойству равнобедренного треугольника:
в равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Т.е.высота BD - это также биссектриса и медиана треугольника АВС.
Поскольку BD - медиана, то AD=DC=½AC= 45÷2= 22,5 см. (АС по условию 45)
Поскольку BD - биссектриса, то углы ABD и CBD равны.
∠ABD=∠CBD=38°. (∠ABD=38° по условию)
∠ABC= ∠ABD+∠CBD= 38°+38°= 76°.
ОТВЕТ: AD=22,5 см, ∠CBD=38°, ∠ABC=76°.
Автор ответа:
4
BD – биссектриса, медиана и высота (т.к. ∆АВС – равнобедренный)
значит, AD=DC=45÷2=22,5см (т.к. АС=AD+DC)
LABD=LCBD=38° (т.к. BD – биссектриса)
значит, LABC=LABD+LCBD=38°+38°=76°
Ответ: LABC=76°; LCBD=38°; AD=22,5см.
Похожие вопросы
Предмет: Русский язык,
автор: НаталиМамаНикиты
Предмет: Английский язык,
автор: МАнуйлова
Предмет: Английский язык,
автор: МАнуйлова
Предмет: Математика,
автор: mirosnichenco5
Предмет: Математика,
автор: daniil242005