Предмет: Алгебра,
автор: emirdautov7
найти
Производную сложной функции
алгебра 10 класс
Приложения:
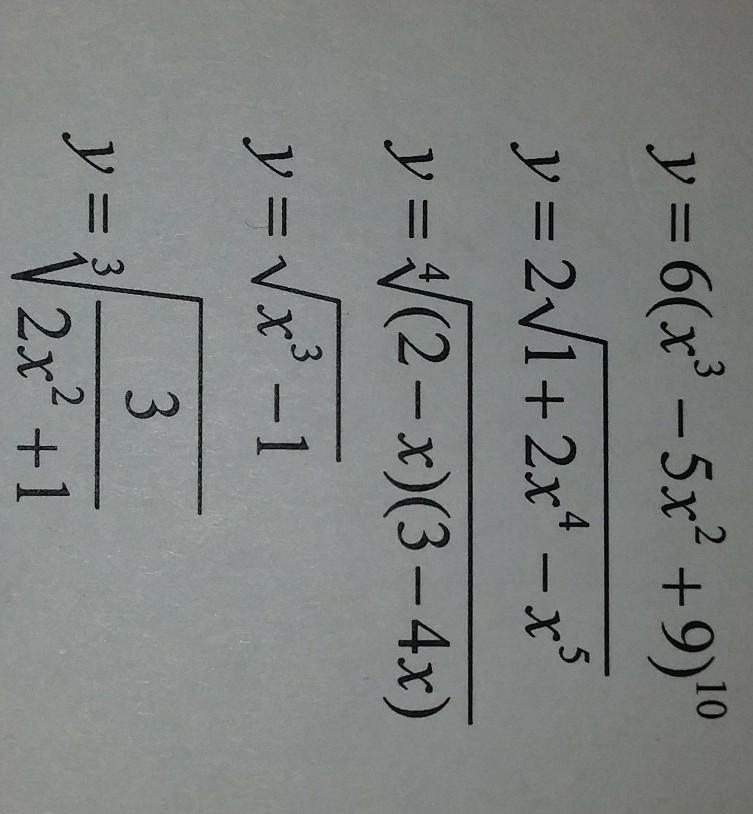
Ответы
Автор ответа:
1
NNNLLL54:
техническая ошибка...
ну я бы не сказал.
а я бы сказала
ваше право
4 sinx забыл - техническая ошибка, а я не увидела 10 из-за перевернутого текста - это не техническая ошибка...
я считаю так, вы - по-другому. Каждый волен думать так, как считает нужным, я вообще не вижу, даже не перевернутого текста.
умейте видеть СВОИ ошибки ...
это сложнее, вот У ВАС приняли ответ. А он все равно с опечаткой. я про интеграл. Странно, почему - то чужие ошибки видее.)))))))
виднее)))
Что вы тут устроили?
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: lampusha79
Предмет: Русский язык,
автор: grandtimon
Предмет: Русский язык,
автор: angelina01
Предмет: Математика,
автор: Червелама
Предмет: Физика,
автор: KJzlZ