Предмет: Алгебра,
автор: bertain
Задание на фотографии
Приложения:

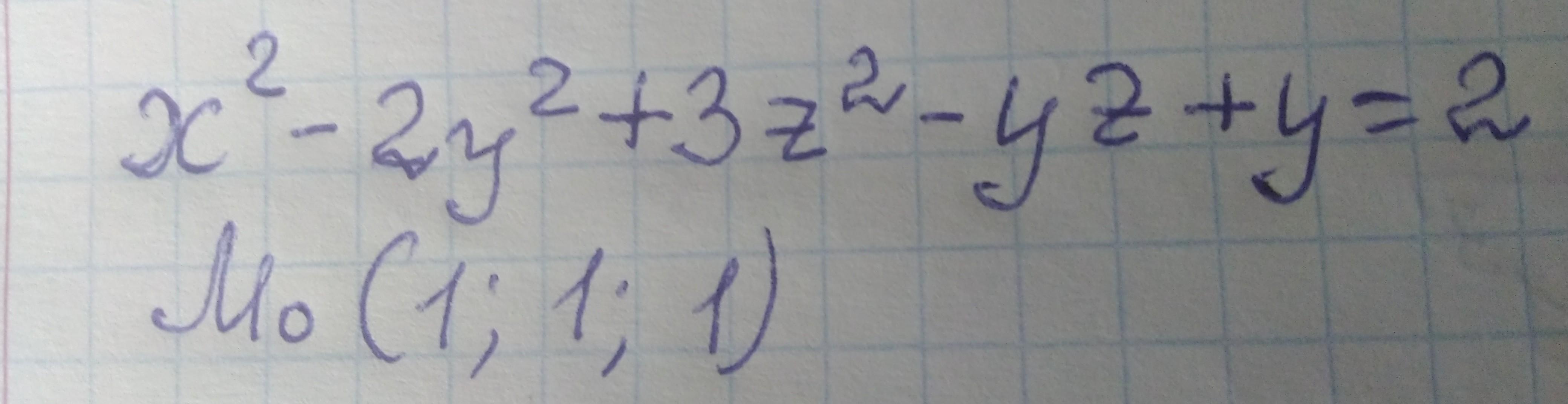
Ответы
Автор ответа:
1
Найдём частные производные
Частные производные в точке (1;1;1).
Похожие вопросы
Предмет: Українська мова,
автор: Vadimysik
Предмет: Українська мова,
автор: 19821982
Предмет: Қазақ тiлi,
автор: anyta0599
Предмет: Математика,
автор: 04042006n
Предмет: Алгебра,
автор: NOOBaSSiK