Предмет: Алгебра,
автор: bertain
Задание на фотографии
Приложения:

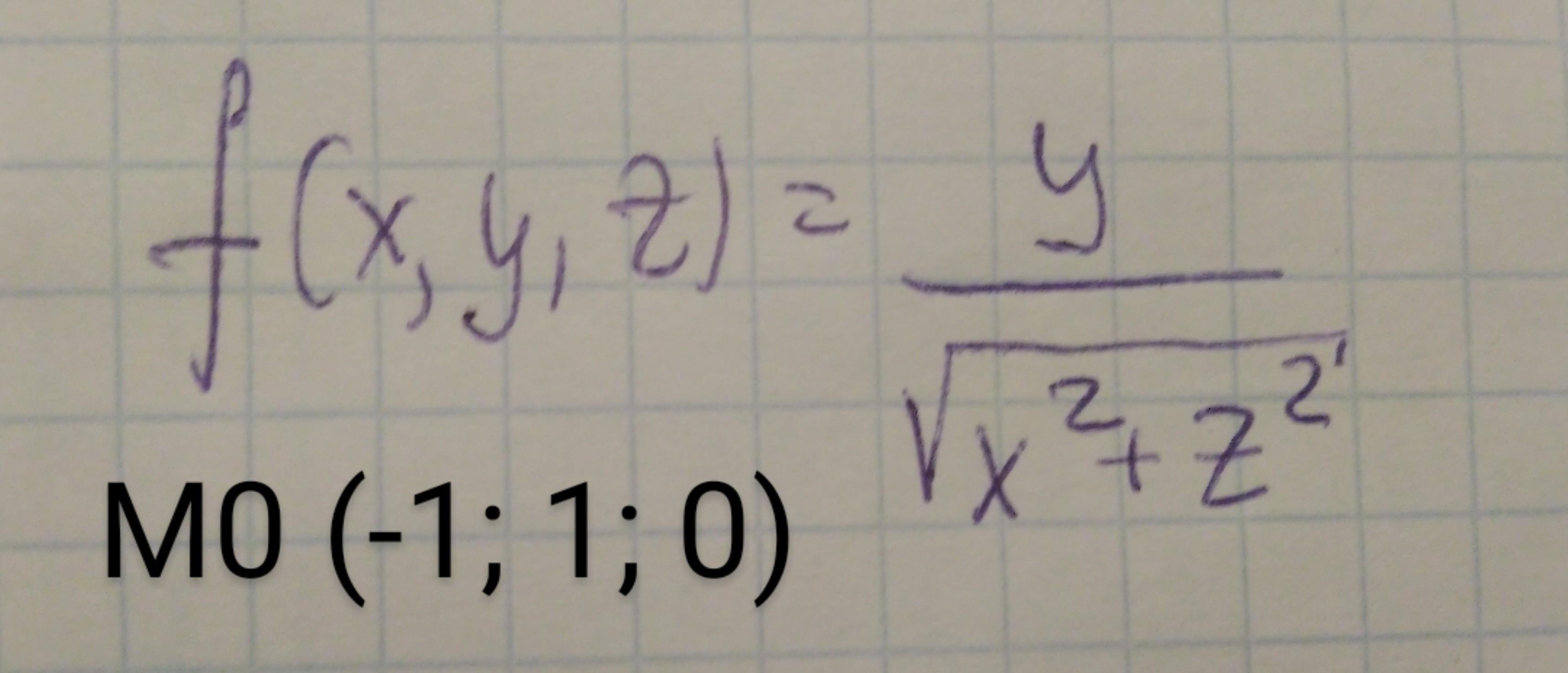
Ответы
Автор ответа:
1
xERISx:
Опечатка в решении : df / dx = +1 - со знаком плюс.
Похожие вопросы
Предмет: Русский язык,
автор: makarena0483
Предмет: Английский язык,
автор: красотка654321
Предмет: Русский язык,
автор: паволочь
Предмет: История,
автор: шира154
Предмет: Алгебра,
автор: Катрин20031