Предмет: Алгебра,
автор: deadbodyson
20 БАЛЛОВ!!! Решить логарифмическое неравенство.
Приложения:
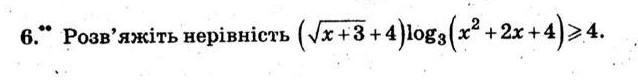
ВладимирБ:
Одз:x>-3;(x+3)^1/2 + 4>=4 при всех допустимых значениях;log(3,x^2+2x+4)>=1 при любом х,=> Ответ:x=[-3;+00)
Ответы
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Исходное условие проверьте: в правой части неравенства 4, а не 0
Значение логарифма надо сравнивать с единицей, а не с нулем...
зрение часто подводит. спасибо.
Автор ответа:
2
Ответ:
[-3; +∞)
Объяснение:
ОДЗ: x + 3 ≥ 0 => x ≥ -3 и x² + 2x+ 4 > 0, для любого х
=> x ≥ -3
рассмотрим множители:
√(x + 3) + 4 ≥ 4 для любого х из ОДЗ
log_3(x² + 2x + 4) ≥ log_3(3) = 1 для любого х из ОДЗ
следовательно произведение всегда ≥ 4 для любого х из ОДЗ
х ∈ [-3; +∞)
x² + 2x+ 4 >0
верно
Похожие вопросы
Предмет: Русский язык,
автор: kydesnik
Предмет: Русский язык,
автор: nazar667
Предмет: Русский язык,
автор: Владимир956
Предмет: Информатика,
автор: Клешер002
Предмет: Информатика,
автор: Аноним