Предмет: Алгебра,
автор: natashalubimova
Помогите решить уравнение sin10x+cos10x=-√2sin8x
Приложения:
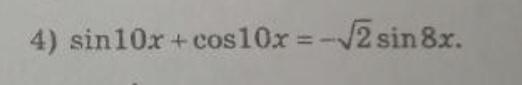
Ответы
Автор ответа:
4
ШереметИрина:
левая часть должна же по формуле сокр.умножения раскрываться(а+b)^2. В общем потеряно удвоенное произведение; + 2sin(10x)cos(10x) (в левой части)
Спасибо за исправление, спешил
Похожие вопросы
Предмет: Русский язык,
автор: Almik
Предмет: Английский язык,
автор: klava78
Предмет: Русский язык,
автор: ПоЗиТиФФчИкМрАк
Предмет: Биология,
автор: ka4ok2