Предмет: Математика,
автор: милашечка24
Помогите пожалуйста решить интеграл неопределенный
Приложения:
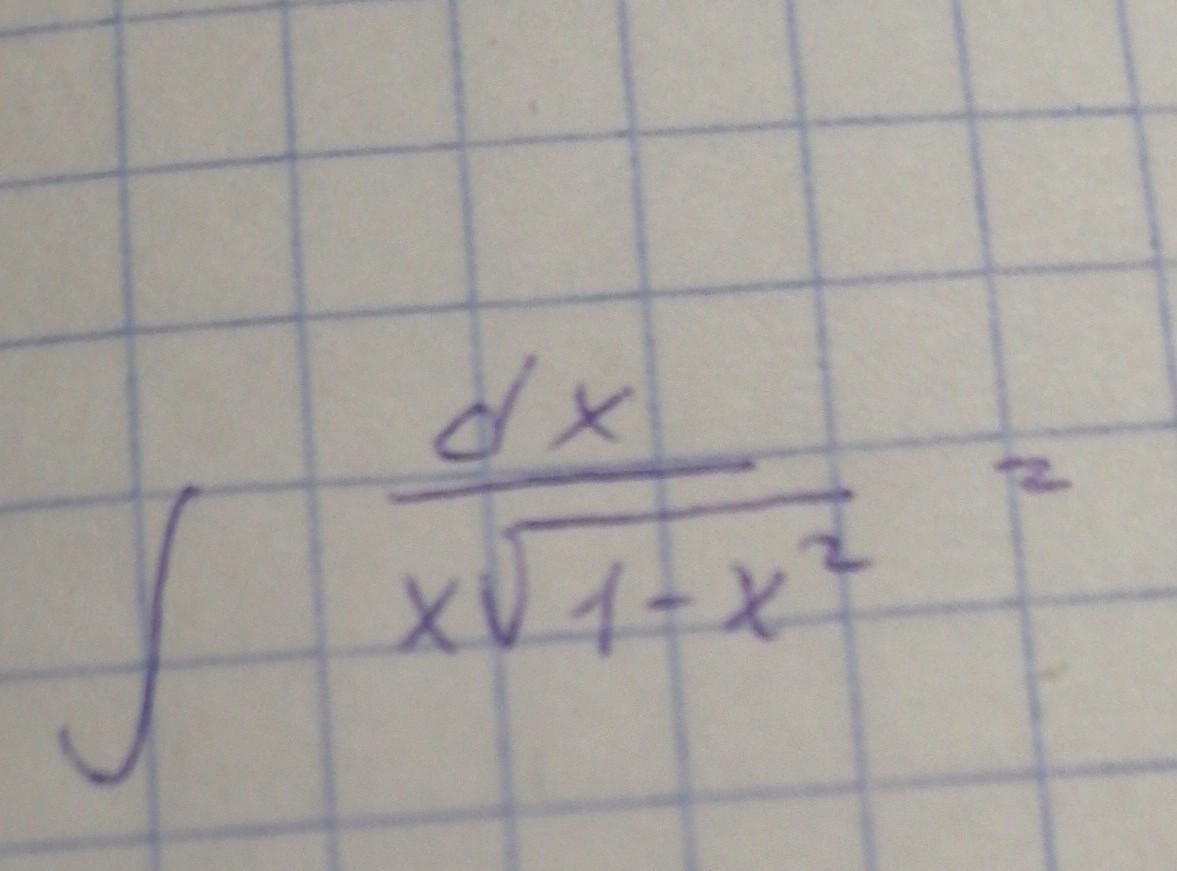
Ответы
Автор ответа:
1
Для вычисления интеграла от дифференциального бинома
где — действительные числа, a
— рациональные числа, также применяется метод подстановки в следующих трёх случаях:
- если
— целое число, то используется подстановка
, где
— общий знаменатель дробей
и
;
- если
, то используется подстановка
, где
— знаменатель дроби
;
- если
, то используется подстановка
, где
— знаменатель дроби
;
Для данного интеграла проверим второй случай: , следовательно, сделаем замену:
. Тогда
и
и
, если
. Имеем:
Сделаем обратную замену:
Ответ: если
Автор ответа:
0
Ответ: во вложении Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: Yu0
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: sylvia2160
Предмет: Математика,
автор: математика531