Предмет: Алгебра,
автор: polyasha29
Найдите корни уравнения методом замены переменной :
Помогите пожалуйста!!!!
Приложения:
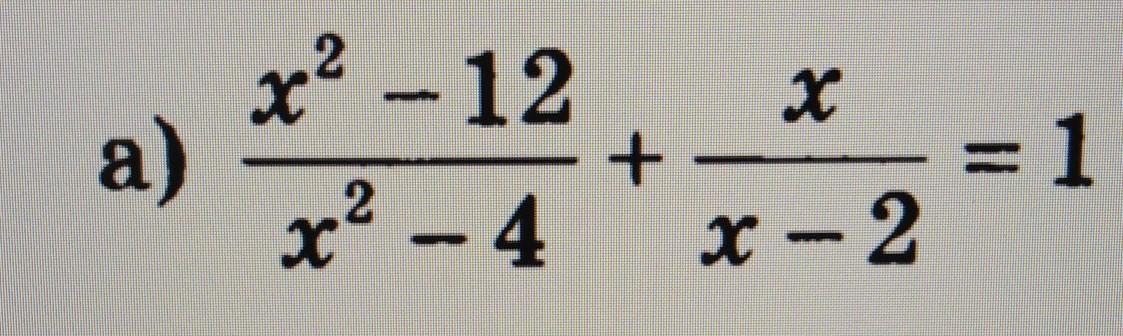
Evgenia4836:
этот метод здесь не к месту
Ответы
Автор ответа:
1
Решение во вложении:
Приложения:

Автор ответа:
2
Похожие вопросы
Предмет: Русский язык,
автор: Stesha35
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: никитоска73
Предмет: История,
автор: nikno10
Предмет: Литература,
автор: juanin