Question

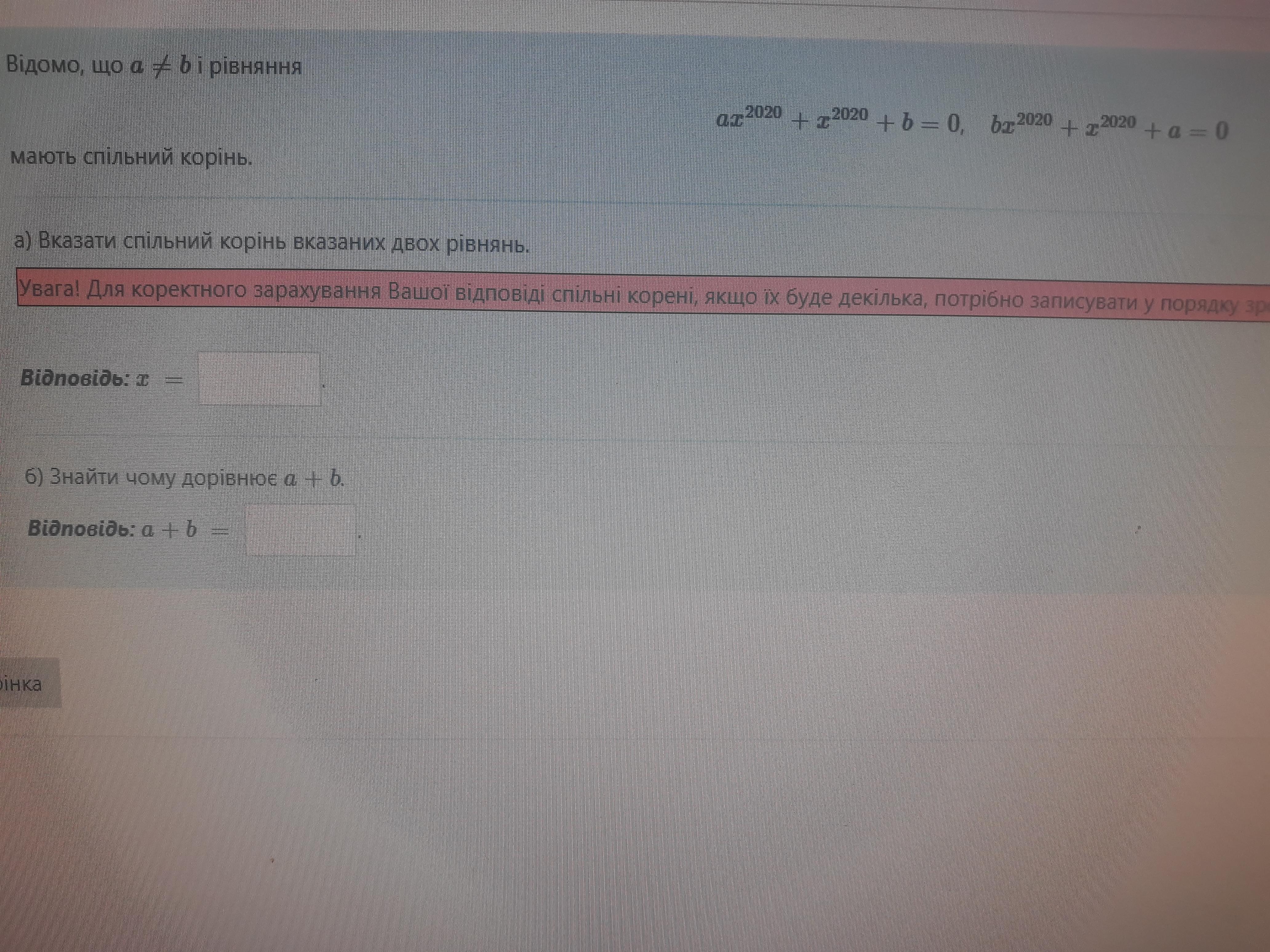
Алгебра сложная неровнасть 35 балов нерівність. Если трудно расписать то можно просто ответ

Answer 1

Для удобства введем замену: $x^{2020}=t, t\geq 0$

Тогда уравнения принимают следующий вид

$at+t+b=0, bt+t+a=0$

Если уравнения имеют общий корень, то существует такое значение $t$, при котором левые части уравнений равны. Приравниваем:

$at+t+b=bt+t+a\\\\at-a-bt+b=0\\\\a(t-1)-b(t-1)=0\\\\(a-b)(t-1)=0\Rightarrow t=1\Leftrightarrow x^{2020}=1\Rightarrow x=\pm1.$

Ответ на пункт $a$ получен.

Для решения пункта $b$ подставим $t=1$  в любое из уравнений (они примут один и тот же вид):

$at+t+b=0\\\\a\cdot1+1+b=0\\\\a+b+1=0\Rightarrow a+b=-1$

ОТВЕТ: $a) -1; 1$.      $b) -1.$