Question

(x^2+6x+5)*(x^2+6x+8)>0​

Answer 1

ax^2 + bx + c = 0

D = b^2 - 4ac

x12 = (-b +- √D)/2a

(x^2+6x+5)*(x^2+6x+8)>0​

раскладываем многочлены

(x^2+6x+5) = (x + 5)(x + 1)

D = 36 - 20 = 16

x12=(-6 +- 4)/2 = -5   -1

(x^2+6x+8) = (x + 2)(x + 4)

D = 36 - 32 = 4

x12 = (-6 +- 2)/2 = -4 -2

(x + 5)(x + 1)(x + 2)(x + 4) > 0

применяем метод интервалов

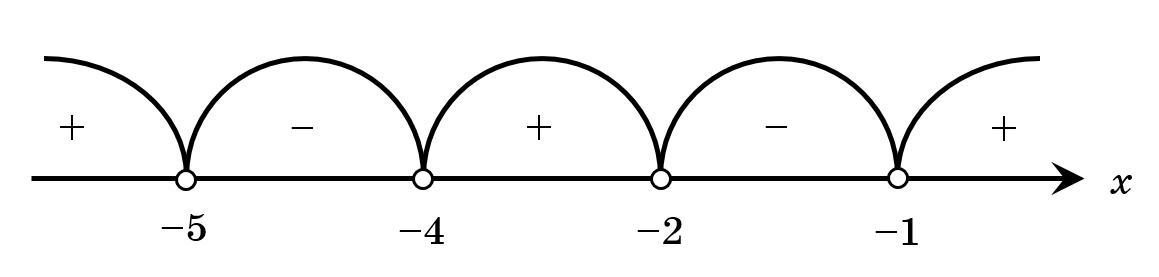
++++++(-5) ---------- (-4) +++++++++ (-2) -------------- (-1) +++++++++

x∈(-∞, -5) U (-4, -2) U (-1, +∞)

Answer 2

$(x^{2} + 6x + 5)(x^{2} + 6x + 8) > 0$

1 способ. Метод интервалов.

Приравняем неравенство к нулю и найдем нули множителей:

$(x^{2} + 6x + 5)(x^{2} + 6x + 8) = 0$

$1) \ x^{2} + 6x + 5 = 0\\x_{1} + x_{2} = -6\\x_{1} \cdot x_{2} = 5\\x_{1} = -5; \ x_{2} = -1$

$2) \ x^{2} + 6x + 8 = 0\\x_{1} + x_{2} = -6\\x_{1} \cdot x_{2} = 8\\x_{1} = -4; \ x_{2} = -2$

Перепишем многочлены вида $ax^{2} + bx + c$ на множители вида $a(x - x_{1})(x - x_{2})$, где $x_{1}$ и $x_{2}$ — корни квадратного уравнения $ax^{2} + bx + c = 0$

Имеем:

$(x + 5)(x + 1)(x+4)(x+2) > 0$

Начертим координатную прямую и отметим выколотыми точками (так как неравенство строгое) нули множителей, и определим знак на каждом интервале ("+", если на этом интервале функция $f(x) = (x + 5)(x + 1)(x+4)(x+2)$ выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.

Следовательно, промежутками, на которых функция $f(x)= (x + 5)(x + 1)(x+4)(x+2)$ больше нуля (выше оси абсцисс), являются:

$x \in (-\infty; -5) \cup (-4; -2) \cup (-1; +\infty)$

2 способ.

Неравенство вида $a \cdot b > 0$ выполняется в двух случаях:

$\left[\begin{array}{ccc}\left\{\begin{array}{ccc}a > 0\\b > 0\\\end{array}\right \\\left\{\begin{array}{ccc}a < 0\\b < 0\\\end{array}\right\\\end{array}\right$

Следовательно, рассмотрим первый случай:

$\left\{\begin{array}{ccc}x^{2} + 6x + 5 > 0\\x^{2} + 6x + 8 > 0\\\end{array}\right$

$\left\{\begin{array}{ccc}(x + 5)(x + 1) > 0\\(x+4)(x + 2) > 0\\\end{array}\right$

Здесь $x = -5$ и $x = -1$ — точки пересечения графика функции $f(x) = x^{2} + 6x + 5$ с осью абсцисс, и  $x = -4$ и $x = -2$ — точки пересечения графика функции $g(x) = x^{2} + 6x + 8$ с осью абсцисс.

Изобразим две параболы для каждого неравенства и определим те абсциссы, при которых каждая из них больше нуля (см. вложение). Имеем промежутки:

$\left\{\begin{array}{ccc}x \in (-\infty; -5) \cup (-1; +\infty)\\x \in (-\infty; -4) \cup (-2; + \infty)\\\end{array}\right$

Следовательно, промежутками, при которых оба неравенства выполняются одновременно, являются:

$x \in (-\infty; -5) \cup (-1; +\infty)$

Рассмотрим второй случай:

$\left\{\begin{array}{ccc}x^{2} + 6x + 5 < 0\\x^{2} + 6x + 8 < 0\\\end{array}\right$

$\left\{\begin{array}{ccc}(x + 5)(x + 1) < 0\\(x+4)(x + 2) < 0\\\end{array}\right$

Из тех же парабол определим те абсциссы, при которых каждая из них меньше нуля:

$\left\{\begin{array}{ccc}x \in (-5; -1)\\x \in (-4; -2)\\\end{array}\right$

Следовательно, промежутком, при котором оба неравенства выполняются одновременно, является:

$x \in (-4; -2)$

Объединим оба случая и получим решение неравенства:

$x \in (-\infty; -5) \cup (-4; -2) \cup (-1; +\infty)$

Ответ: $x \in (-\infty; -5) \cup (-4; -2) \cup (-1; +\infty)$