Question

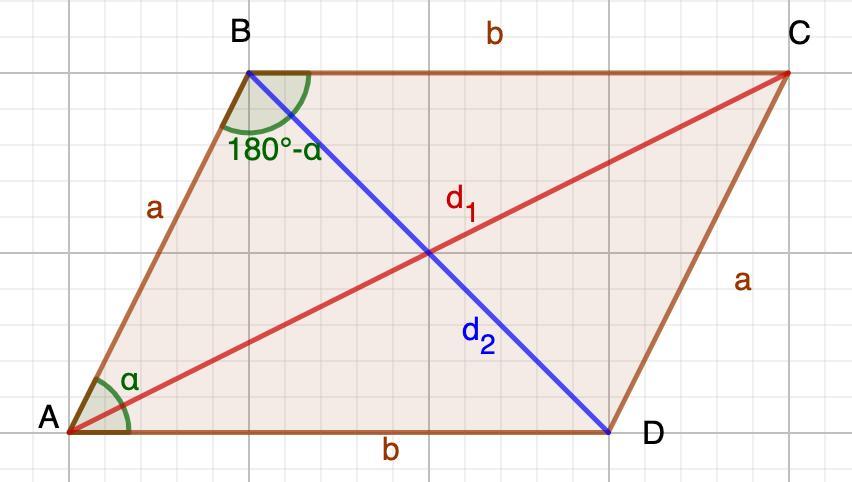
Доведіть що сума квадратів діагоналей паралелограма дорівнює сумі квадратів усіх його сторін.

Answer 1

Ответ:

Объяснение:

Противоположные стороны параллелограмма равны.

Сумма углов параллелограмма прилежащих к одной стороне равна 180°.

Теорема косинусов:

$c^2=a^2+b^2-2ab*cos\alpha$

Формула приведения:

$cos(180^o-\alpha )=-cos\alpha$

Используя теорему косинусов, выразим квадраты диагоналей:

$d_1^2=a^2+b^2-2ab*cos(180^o-\alpha )\\d_2^2=a^2+b^2-2ab*cos\alpha$

Преобразуем первое выражение, используя формулу приведения и сложим два полученных равенства:

$d_1^2=a^2+b^2+2ab*cos\alpha \\d_2^2=a^2+b^2-2ab*cos\alpha\\\\------------\\d_1^2+d_2^2=2a^2+2b^2+2ab*cos\alpha -2ab*cos\alpha \\d_1^2+d_2^2=a^2+a^2+b^2+b^2$