Question

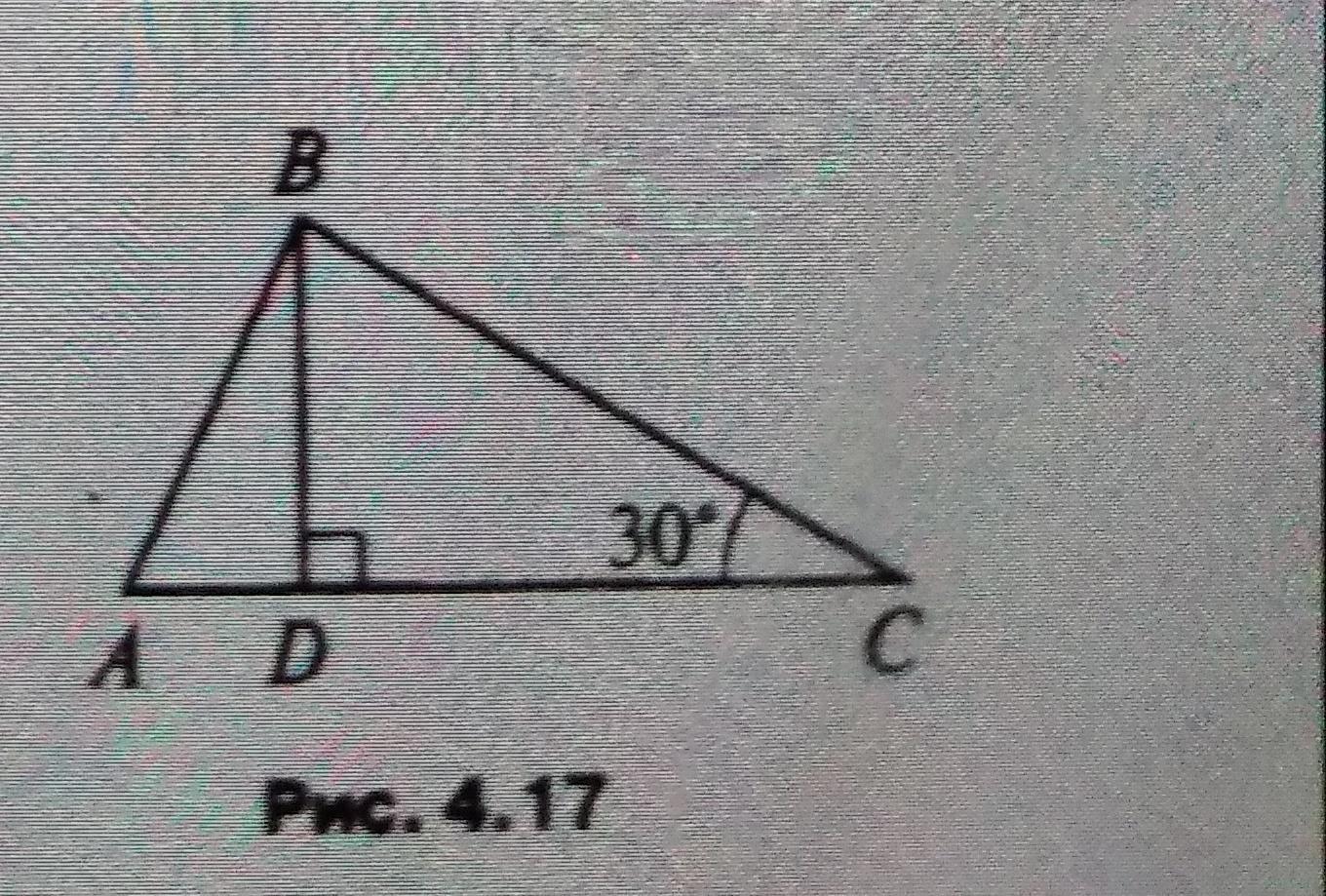
BC=AC
найти: угол ABD

Answer 1

Ответ:

15°

Объяснение:

BC = AC => ∠B = ∠A = (180-30)/2 = 75;

∠CBD = 180 - 30 - 90 = 60 =>

=> ∠ABD = ∠B-∠CBD = 15°

Answer 2

Ответ:

$\displaystyle \tt \angle ABD =15^{\circ}$

Объяснение:

1) Так как $\displaystyle \tt BC=AC$, то $\displaystyle \tt \triangle ABC$ - равнобедренный (по определению)

2) Так как $\displaystyle \tt \triangle ABC$ - равнобедренный, то $\displaystyle \tt \angle CBA= \angle CAB$ (по свойству)

3) Так как $\displaystyle \tt \angle CBA= \angle CAB$, то найдём $\displaystyle \tt \angle BAC$:

$\displaystyle \tt \angle BAC=\frac{180^{\circ}-30^{\circ}}{2}=\frac{150^{\circ}}{2}=75^{\circ}$

4) Так как $\displaystyle \tt BD$ - высота, то $\displaystyle \tt \angle BDA=90^{\circ}$, следовательно $\displaystyle \tt \triangle ABD$ - прямоуг.

5) Так как $\displaystyle \tt \angle BAD=75^{\circ}$, то по теореме о сумме острых углов в прямоугольном треугольнике найдём $\displaystyle \tt \angle ABD$:

$\displaystyle \tt \angle ABD=90^{\circ}-\angle BAC=90^{\circ}-75^{\circ}=15^{\circ}$