Предмет: Математика,
автор: quarckium
Если можно решите пожалуйста очень хочу понять как решаеться подобное.
Приложения:
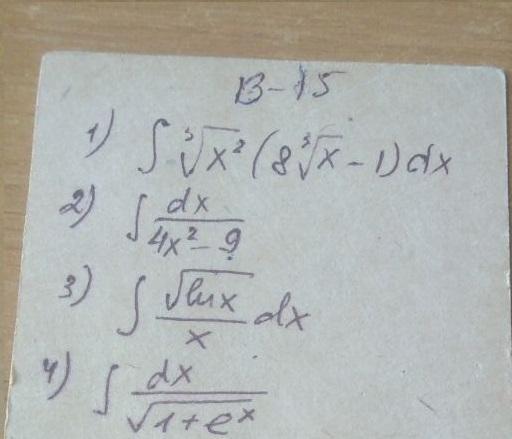
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: талаб
Предмет: Английский язык,
автор: remark2012
Предмет: Английский язык,
автор: kristina789
Предмет: Математика,
автор: Aiisha3
Предмет: Обществознание,
автор: sveta2312