Предмет: Алгебра,
автор: Cipcilinka
Найти значения выражений с кв. корнями. С решением
Приложения:
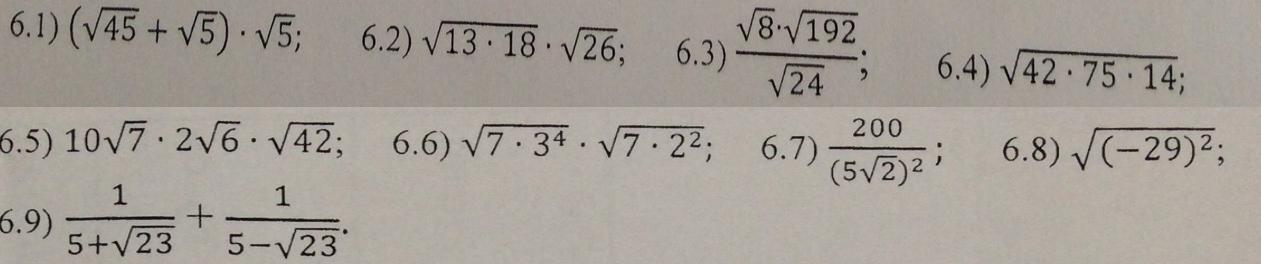
Ответы
Автор ответа:
1
Автор ответа:
0
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: Tanja123
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: nastasia2321
Предмет: Математика,
автор: AlinaFedi