Предмет: Алгебра,
автор: Аноним
Решить биквадратное уравнение:
x^4-12x^2-64=0
Ответы
Автор ответа:
1
.....................
Приложения:
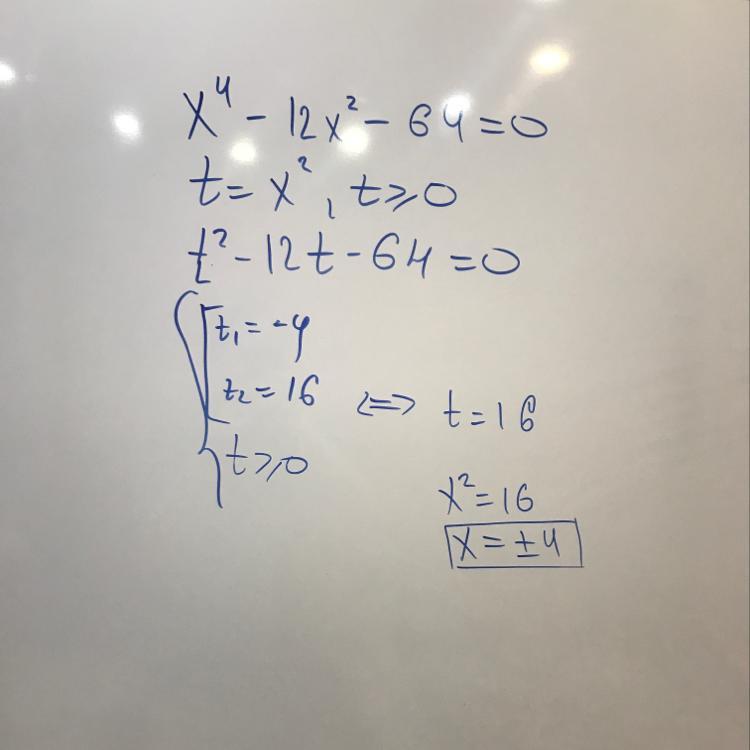
Автор ответа:
2
Пусть , тогда:
- нет корней
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Салахов
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: berkova
Предмет: История,
автор: ymnayagolova
Предмет: Математика,
автор: данил1530