Предмет: Алгебра,
автор: aronkardumovic
Сократить дроби, даю 35 баллов
Приложения:
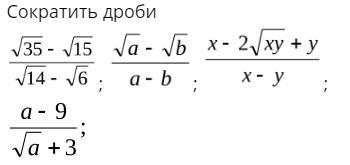
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1)
2)
3)
4)
Похожие вопросы
Предмет: Английский язык,
автор: caroline9868
Предмет: Русский язык,
автор: okea
Предмет: Русский язык,
автор: Джамай
Предмет: Математика,
автор: хорошистка176
Предмет: Биология,
автор: alics26