Предмет: Алгебра,
автор: VeroNikaG19
решите уравнения, 30 баллов!
Приложения:
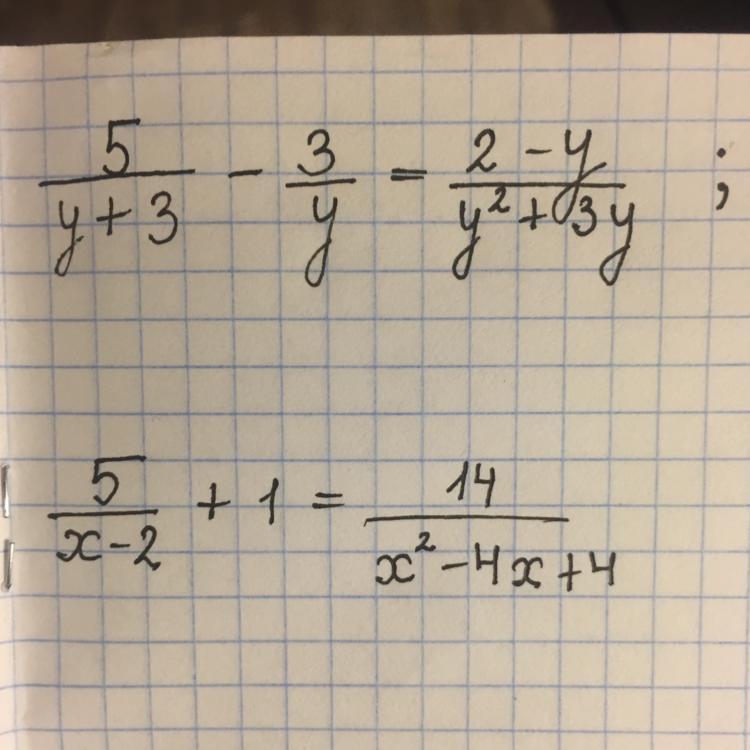
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Русский язык,
автор: snow962606
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: максюшик
Предмет: Математика,
автор: крисс22
Предмет: Алгебра,
автор: xxxx39