Предмет: Математика,
автор: ТатМих
Проинтегрировать дифференциальное уравнение.
При заданном начальном условии найти соответствующий частный интеграл или частное решение.
номер 394
Приложения:
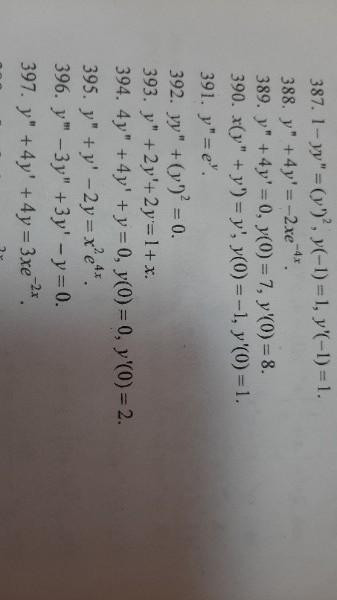
Ответы
Автор ответа:
3
Ответ: y=2*x*e^(-1/2*x).
Пошаговое объяснение:
Составляем характеристическое уравнение: 4*k²+4*k+1=0. Оно имеет равные корни k1=k2=-1/2, поэтому данное дифференциальное уравнение имеет общее решение y=C1*e^(-1/2*x)+C2*x*e^(-1/2*x). Дифференцируя его, находим y'=-1/2*C1*e^(-1/2*x)+C2*e^(-1/2*x)-1/2*C2*x*e^(-1/2*x). Используя условия y(0)=0 и y'(0)=2, получаем систему уравнений:
C1=0
-1/2*C1+C2=2, откуда C2=2. Тогда искомое частное решение y=2*x*e^(-1/2*x).
Похожие вопросы
Предмет: Русский язык,
автор: хонда
Предмет: Английский язык,
автор: ане4444ка
Предмет: Русский язык,
автор: Lizagosteva220701
Предмет: Математика,
автор: solodovnikova100503
Предмет: Математика,
автор: СуXаРиК