Предмет: Алгебра,
автор: Kaimoldenov
Помогите решить!!!!
Приложения:
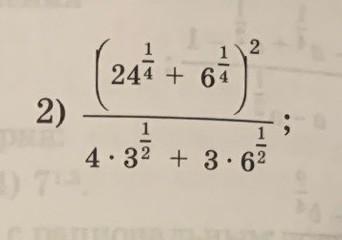
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: SpLiT
Предмет: Русский язык,
автор: abylkan
Предмет: Українська мова,
автор: vikaklevak
Предмет: Математика,
автор: ева383