Предмет: Алгебра,
автор: otari
Вычислить площадь фигуры,Вычислить площадь фигуры, ограниченной линиями. A) y=-x2(в квадрате) + 4 Y=0 b) y=-x2(в квадрате) + 4 Y=4 Помогите пожалуйста. Если не затруднит, то напишите подлробно.
Ответы
Автор ответа:
0
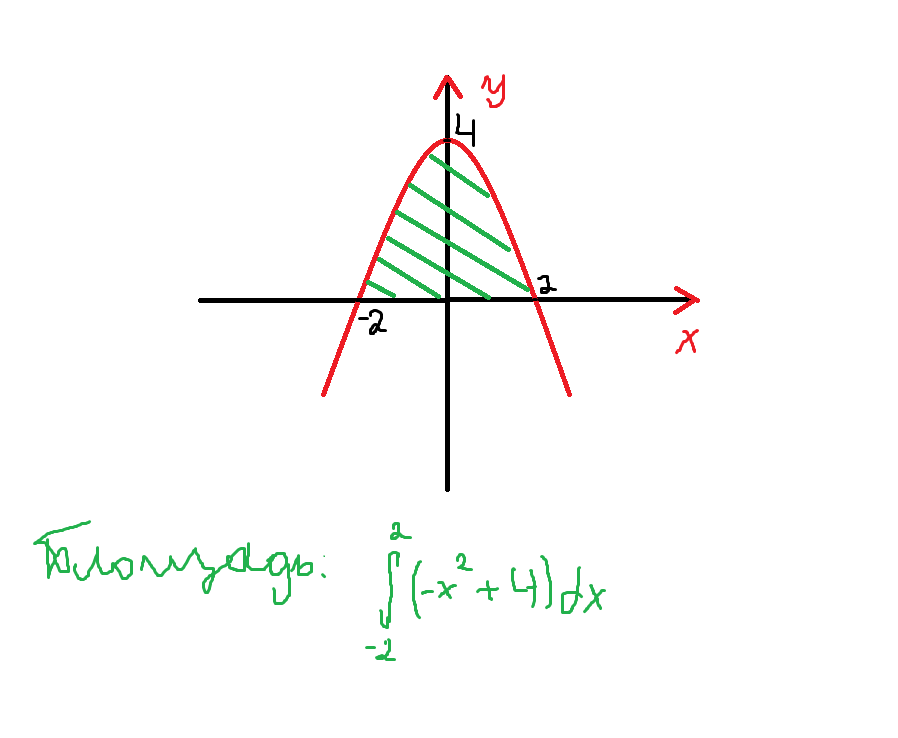
a) Нашей задачей на самом деле является нахождение определенного интеграла от функции на каком-то промежутке, потому что определенный интеграл представляет собой площадь под графиком функции (т.е. между графиком и прямой  )
)
В общем случае, нужно решить уравнение чтобы найти те точки, где график пересекает прямую
чтобы найти те точки, где график пересекает прямую  . В нашем случае несложно догадаться, что
. В нашем случае несложно догадаться, что  пересекает ее в
пересекает ее в  ,
, 
Итак:

Ответ: площадь фигуры равна 32/3 кв. ед
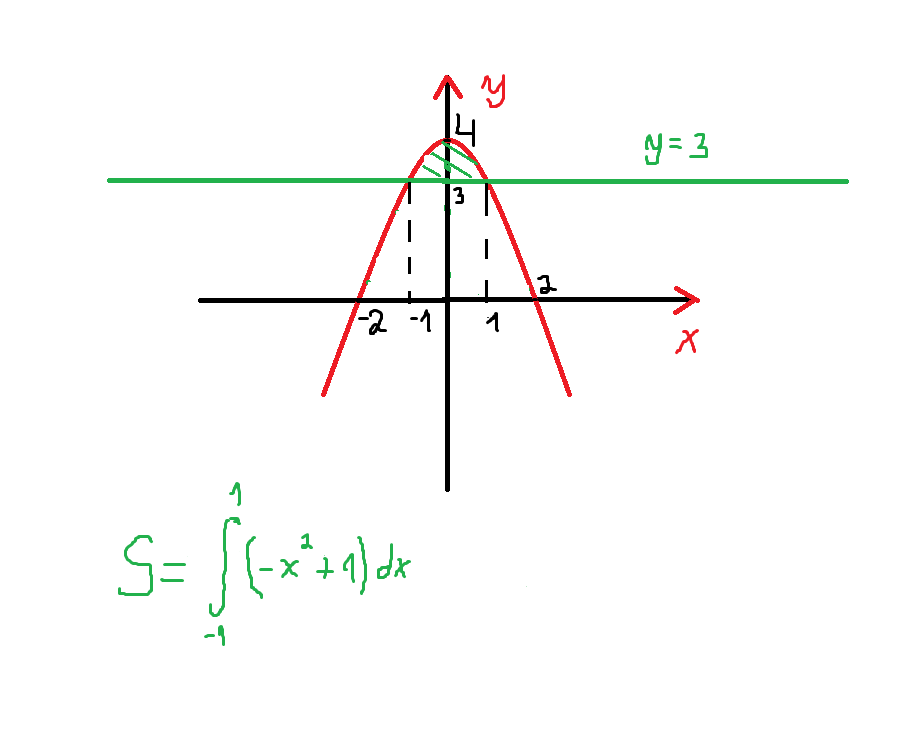
б) Эта задача сводится к вычислению следующего интеграла (как видно из рисунка 2):

Ответ: площадь искомой фиругы равна 4/3.
В общем случае, нужно решить уравнение
Итак:
Ответ: площадь фигуры равна 32/3 кв. ед
б) Эта задача сводится к вычислению следующего интеграла (как видно из рисунка 2):
Ответ: площадь искомой фиругы равна 4/3.
Приложения:
Автор ответа:
0
Спасибо, братишка. Спасибо большое.
Похожие вопросы
Предмет: Алгебра,
автор: grauerliliya
Предмет: История,
автор: lisalike122
Предмет: Русский язык,
автор: lanatsiganok
Предмет: Математика,
автор: ilonka12