Предмет: Алгебра,
автор: Mr0leg
Вычислить интеграл функции, №1
Приложения:
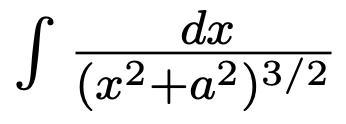
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: 678446
Предмет: Русский язык,
автор: 1092000
Предмет: Русский язык,
автор: Yanushka
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Мила960