Question

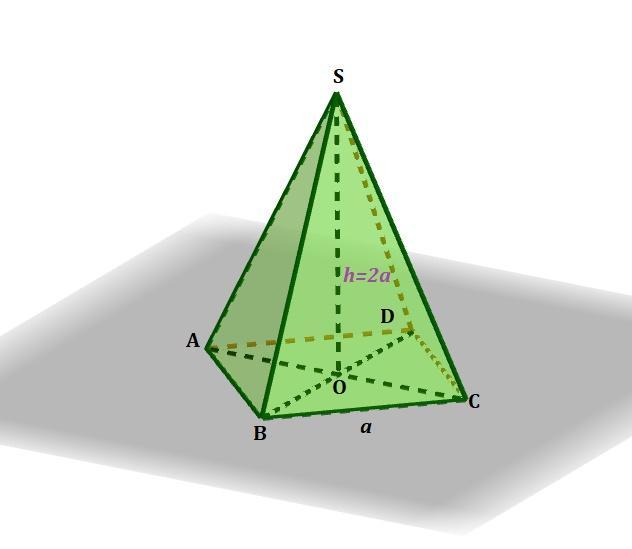
Площа основи правильної чотирикутної піраміди дорівнює 36 см2 . Визначте об’єм цієї піраміди, якщо її висота вдвічі більша за сторону основи

Answer 1

Ответ:

Об’єм цієї піраміди дорівнює 144 м³

Пошаговое объяснение:

Площа основи правильної чотирикутної піраміди дорівнює 36 см² . Визначте об’єм цієї піраміди, якщо її висота вдвічі більша за сторону основи.

• Правильною чотирикутною пірамідою називається піраміда, основою якої є квадрат, а бічні грані - рівнобедрені трикутники.

Вершина піраміди проектується в точку перетину діагоналей основи (квадрата).

Дано: ABCDS - правильна піраміда. Основа ABCD - кадрат. АВ=ВС=СD=AD. $S_{ABCD}=$ 36 см², SO - висота піраміди, SO=2АВ.

Знайти: $\bf V_{ABCDS} - ?$  

Так як в основі правильної чотирикутної піраміди  лежить квадрат, то площа основи знаходиться за формулою:

S=a²

а -  сторона квадрата.

S=36 - за умовою,

звідки а=АВ =6 см.

Тоді висота піраміди SO= 2⋅АВ=2·6=12 см.

Об'єм піраміди знаходимо за формулою:

$\boxed{\bf V=\frac{1}{3}Sh }$

Маємо:

V=36⋅12:3=36⋅4=144 см³.

#SPJ5