Предмет: Алгебра,
автор: mariysado22
Решите, пожалуйста, пример из вложения.
Приложения:
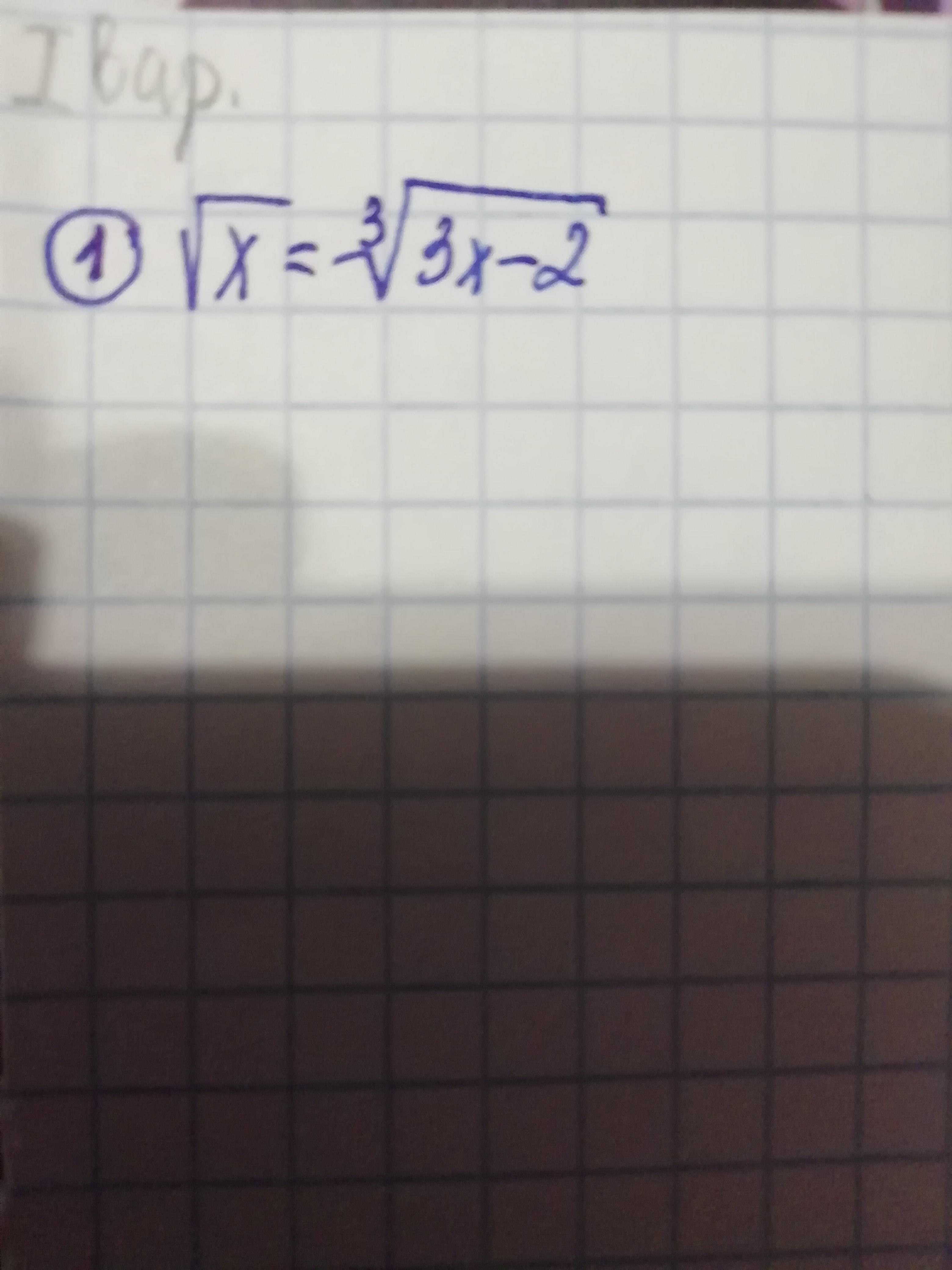
Ответы
Автор ответа:
0
Ответ:
Умножаем на 6 степень :
При этом 3x-2 больше или равно нулю и x больше или равно нулю.
По формуле Герона x1 = 1
(x - 1)(x² – 8x + 4) = 0
D=8²-4×4×1 = 64-16 = 48
Аналогичным образом:
При проверке выясняется, что при использовании второго корня выражение не имеет смысла.
В ответе запишите только x1 и x3.
EvilROMA:
Система немного сломалась, но в общем: при постановке второго корня в условия под корнями выражение не имеет смысла
Извините, утверждение выше оказалось некорректно
Похожие вопросы
Предмет: Русский язык,
автор: kz2
Предмет: Английский язык,
автор: viktor101211
Предмет: Русский язык,
автор: ghh99
Предмет: Литература,
автор: кирик61
Предмет: География,
автор: shadia