Предмет: Математика,
автор: cthsq0805
Прямые x= 3 и y = 1 являются касательными к окружности.
данной уравнением (х - хо) + (у - у) = 25. Найдите координаты центра окружности.
Ответы
Автор ответа:
15
Ответ:
(8;6), (8;-4), (-2;6) и (-2;-4)
Пошаговое объяснение:
(x-x₀)²+(y-y₀)²=25 - уравнение окружности
(x-x₀)²+(y-y₀)²= 5²
R=5 - радиус окружности
Находим координаты центра окружности, если прямые х=3 и у=1 являются касательными к окружности.
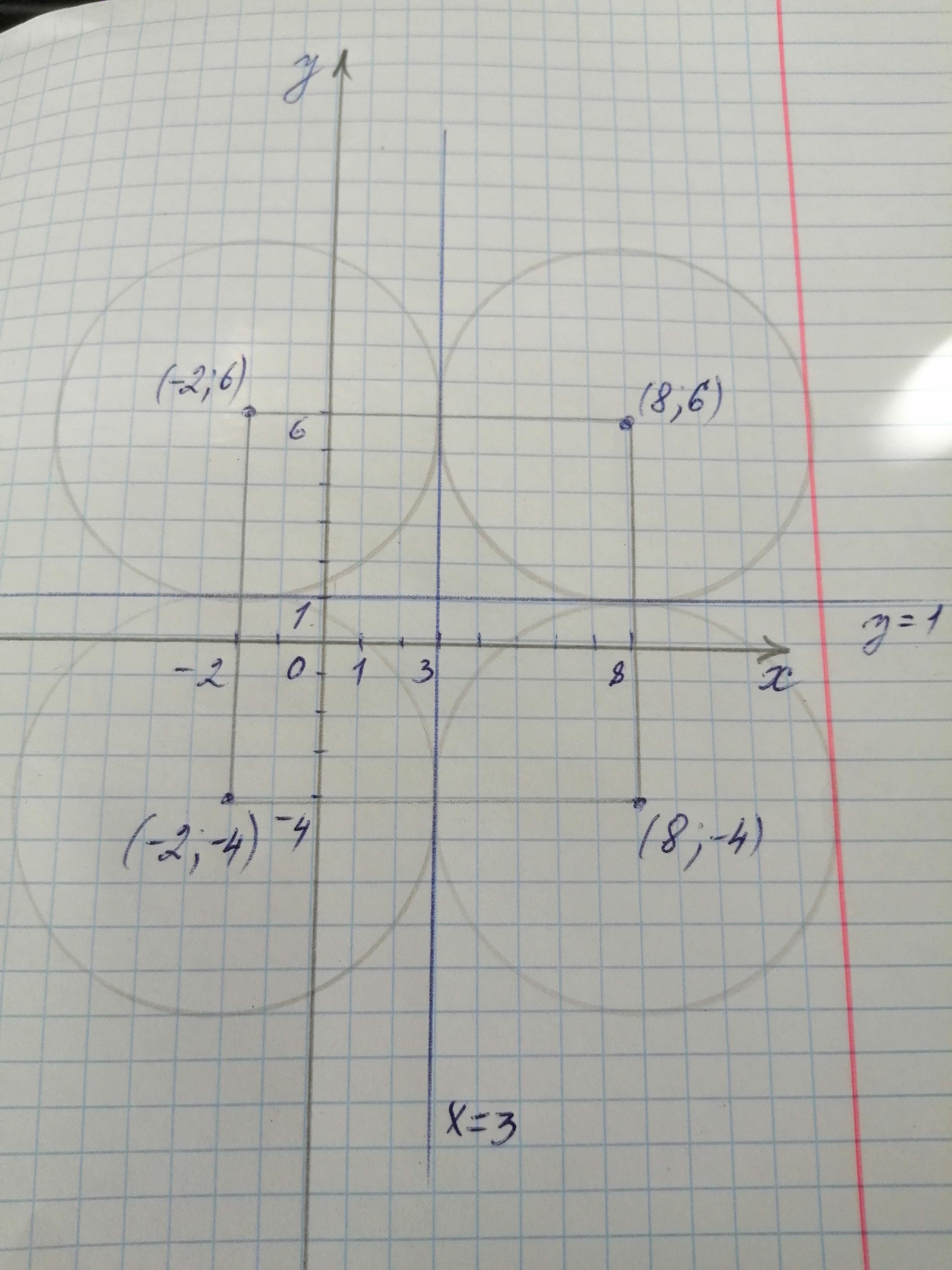
Рассмотрим рисунок (в приложении). На нём система координат Оху, прямые х=3 и у=1. На рисунке показано, что окружностей, которые могут касаться данных прямых на самом деле 4. Учитывая, что радиус окружности равен 5, находим координаты центров этих окружностей.
Касательные х=3 и у=1 пересекаются в точке (3;1). От этой точки вправо, влево, вверх и вниз отсчитываем по 5 единиц.
3+5=8
3-5=-2
1+5=6
1-5=-4
Получаем точки (8;6), (8;-4), (-2;6) и (-2;-4), которые и являются центрами окружностей.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 12345sanya12345
Предмет: Русский язык,
автор: 24200101
Предмет: Русский язык,
автор: ksanaT
Предмет: Математика,
автор: igorshik
Предмет: Обществознание,
автор: frgndjbgjnhxj