Предмет: Алгебра,
автор: darkomarco
задачи с логарифмами (1 а б в г)
Приложения:
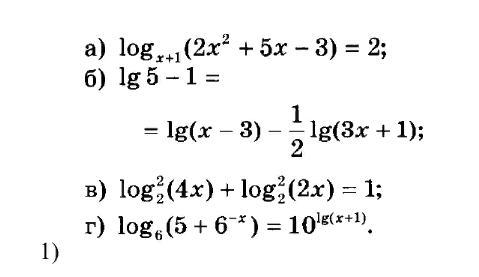
Ответы
Автор ответа:
1
1)
решаем методом рационализации
Ответ : х=1
2)
Ответ : х= 5
3)
4)
Похожие вопросы
Предмет: Английский язык,
автор: nastianicho
Предмет: Русский язык,
автор: 1999198020011977
Предмет: Русский язык,
автор: Lolai
Предмет: Математика,
автор: Илья5111111