Предмет: Математика,
автор: aigerim5330
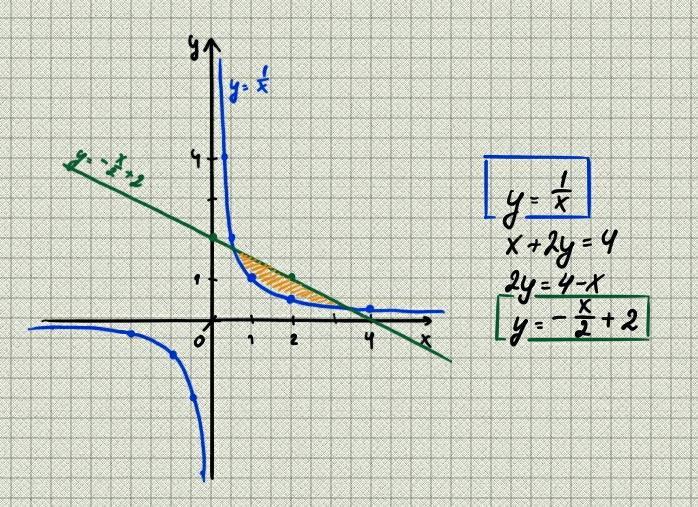
Найдите площадь фигуры ограниченной линиями: y=1/x,x+2y=4
Ответы
Автор ответа:
1
Пошаговое объяснение:
Изображение фигуры, которую нужно найти, во вложении.
Найдём абсциссы точек пересечения графиков функций:
Это будут границы интегрирования.
Так как линейная функция выше, чем ветвь гипербола (в рассматриваемом промежутке), то для нахождения площади будем последнюю вычитать, то есть:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Пе4енька1909
Предмет: Русский язык,
автор: анабель2002
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Ariha505
Предмет: Математика,
автор: diring00