Предмет: Геометрия,
автор: romabryuxachev
СРочноооооооооо!!!!!!!!!!!!!!!!!!!!!!
Приложения:
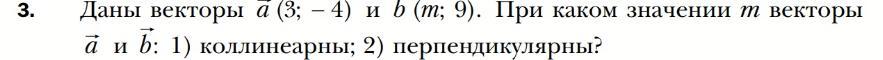
TEOPEMA1:
надеюсь успел и ничего не напутал
и везде там стрелочки ставь над a И b, иначе училка(тель) будет ругаться.
даны векторы a(3; -4) и b(m; 9). При каком значении m векторы a и b: 1) коллинеарны; 2) перпендикулярны?
да
Ответы
Автор ответа:
1
Ответ:
при m=-6,75 векторы коллинеарны.
при m=12 векторы перпендикулярны (ортогональны)
Объяснение:
есть условие коллинеарности векторов:
вот и найдём неизвестный нам b1 из этого условия методом пропорций.
b1 это m
m=b1= (Коллинеарны)
Теперь найдем значение m(b1), при котором векторы перпендикулярны.
Векторы будут перпендикулярны друг другу, если их скалярное произведение будет равно нулю.
составим уравнение из этого условия:
(a, b) = 3*m+(-4)*9 = 3m+(-36) = 3m-36
из условия выше, что произведение равно нулю получаем:
3m-36=0
3m=36
m=12 (Перпендикулярны)
помоги это еще Даны векто�ы m(4;14) и n(-7;k) при каком значении k векторы m и n : 1) коллинеарны, 2) перпендикулярны
пожалуйста оч прошу
без длинного решения только: k=(-7*14):4=-24,5 - коллинеарны
теперь перпендикулярный найдём:
(a,b)=4*(-7)+14*k=-28+4k
-28+4k=0
4k=28
k=28:4
k=7 - перпендикулярны
теперь перпендикулярный найдём:
(a,b)=4*(-7)+14*k=-28+4k
-28+4k=0
4k=28
k=28:4
k=7 - перпендикулярны
Похожие вопросы
Предмет: Русский язык,
автор: АнЪко
Предмет: Другие предметы,
автор: АнЪко
Предмет: Английский язык,
автор: Elzok
Предмет: Математика,
автор: sofiika04012