Предмет: Математика,
автор: HopiTakeo
Дан неопрелеленный интеграл. Найти интеграл
Приложения:
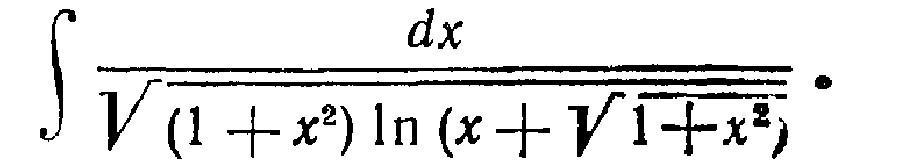
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: cher7943
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Насяся
Предмет: География,
автор: izibaevsergei
Предмет: Математика,
автор: наталья604