Решите уравнения 8 класс. Через дискреминант
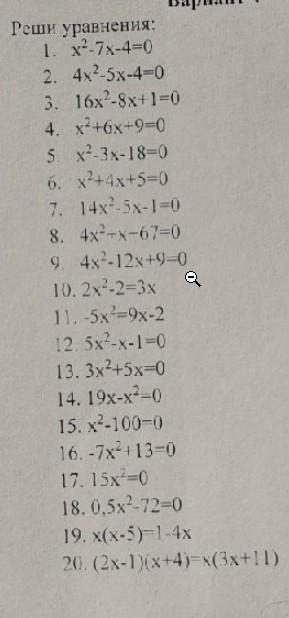
Ответы
Ответ:
Пошаговое объяснение:
1. х²-7х-4=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-7)² - 4·1·(-4) = 49 + 16 = 65
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁= 7 - √65/ 2·1 ≈ -0.53113
x₂ = 7 + √65/ 2·1 ≈ 7.5311
2.
4x² - 5x - 4 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-5)² - 4·4·(-4) = 25 + 64 = 89
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = 5 - √89/ 2·4 ≈ -0.55425
x₂ = 5 + √89/ 2·4 ≈ 1.8042
3.
16x² - 8x + 1 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-8)² - 4·16·1 = 64 - 64 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительный корень:
x = 8 /2·16 = 0.25
4.
х²+6х+9=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 6² - 4·1·9 = 36 - 36 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительный корень:
x = -6 /2·1 = -3
5.
х²-3х-18=0
По теореме Виета
х₁+х₂=3
х₁х₂= -18
х₁= -3
х₂=6
6.
х²+4х+5=0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 4² - 4·1·5 = 16 - 20 = -4
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
7.
14x² - 5x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = (-5)² - 4·14·(-1) = 25 + 56 = 81
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = 5 - √81/ 2·14 = 5 - 9/ 28 = -4 /28 = - 1 /7
x₂ = 5 + √81 /2·14 = 5 + 9 /28 = 14 /28 = 0.5
8.
4x² + x - 67 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 1² - 4·4·(-67) = 1 + 1072 = 1073
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁= -1 - √1073/ 2·4 ≈ -4.2
x₂ = -1 + √1073/ 2·4 ≈ 4