Предмет: Алгебра,
автор: nnnnnnnkk7
решить логарифмические неравенста
Приложения:
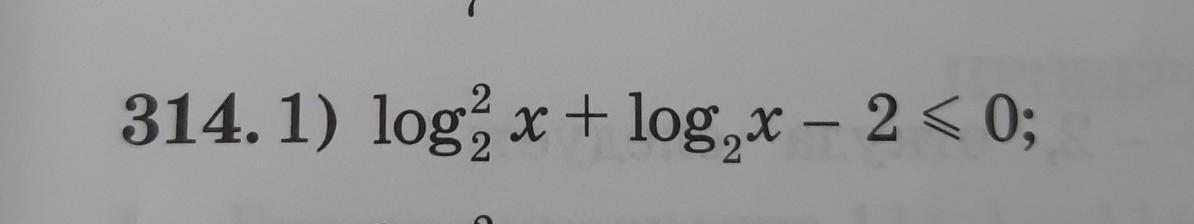
Ответы
Автор ответа:
1
log2(x) = t
t²+t-2 <= 0
t²+2t-t-2 <= 0
t(t+2)-1(t+2) <= 0
(t+2)(t-1) <= 0
+. -. +
-----------[-2]--------------[1]------------
-2 <= t <= 1
-2 <= log2(x) <= 1
2^(-2) <= 2^(log2(x)) <= 2^1
1/4 <= x <= 2
Ответ: [1/4; 2]
Похожие вопросы
Предмет: Русский язык,
автор: ZinkaKalinka
Предмет: Українська мова,
автор: vbnm528
Предмет: Русский язык,
автор: lidush
Предмет: Математика,
автор: ЛИАК
Предмет: Обществознание,
автор: Лера5акласс