Предмет: Алгебра,
автор: Serfcort
Докажите неравенство
Приложения:
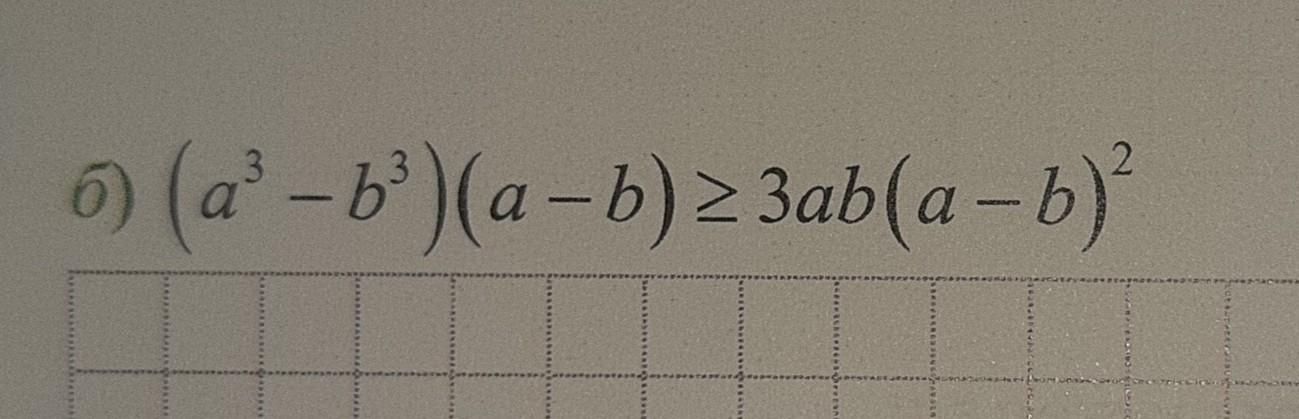
Ответы
Автор ответа:
1
Ответ:
Объяснение:
число в четной степени ≥0, неравенство верно
Похожие вопросы
Предмет: Русский язык,
автор: omar123
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Мишелька000
Предмет: История,
автор: sofya160
Предмет: Биология,
автор: m1ndess1