Предмет: Алгебра,
автор: Cutieplay
Решите пожалуйста задачу:
Площадь прямоугольника 96см в квадрате . Найдите его стороны,если одни из них на 4 см меньше другой.
И решите уравнение
x^4 - 3x^2 - 4 = 0
Ответы
Автор ответа:
0
Ответ:
Решения заданий на листочке
Приложения:
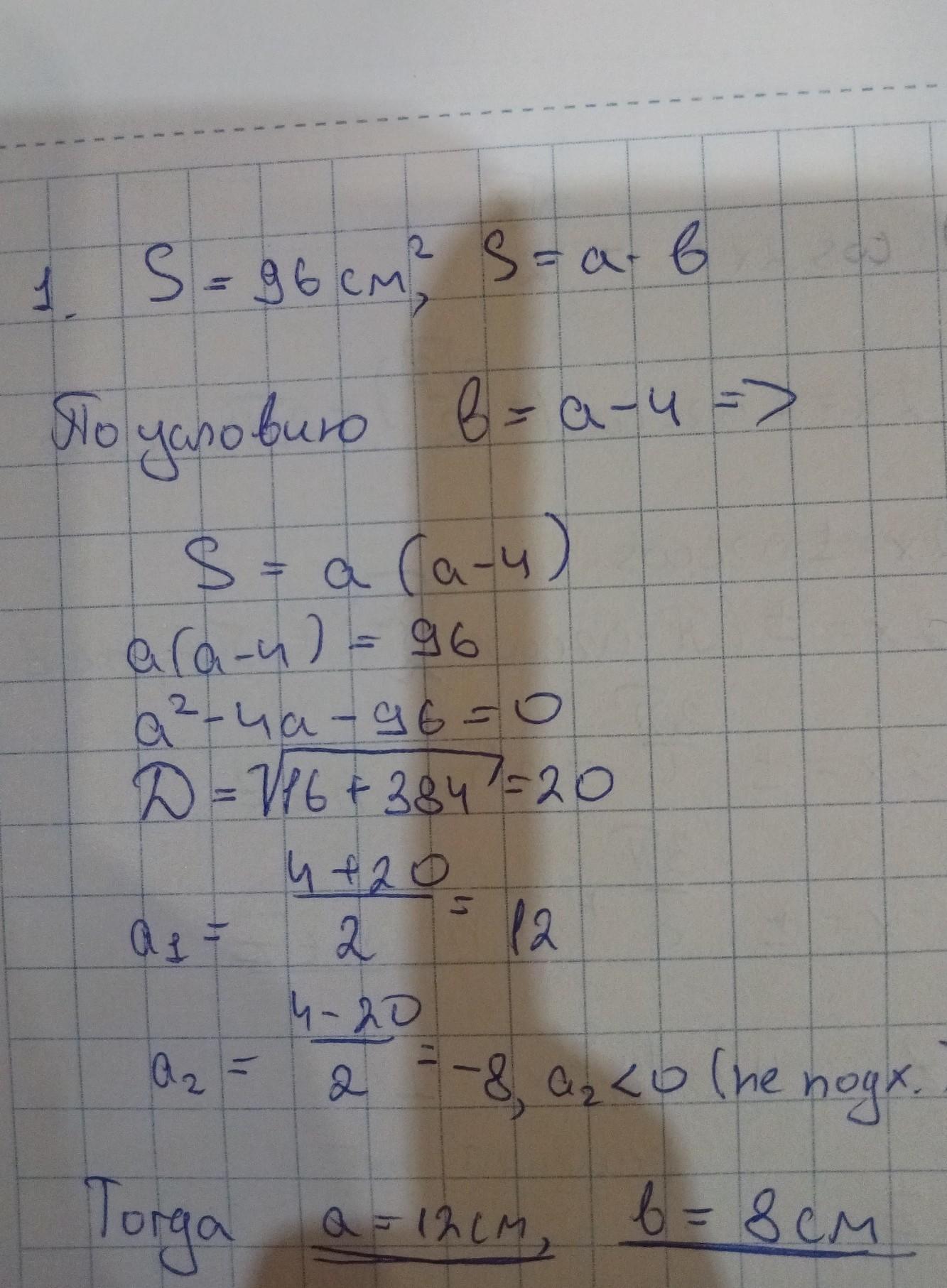
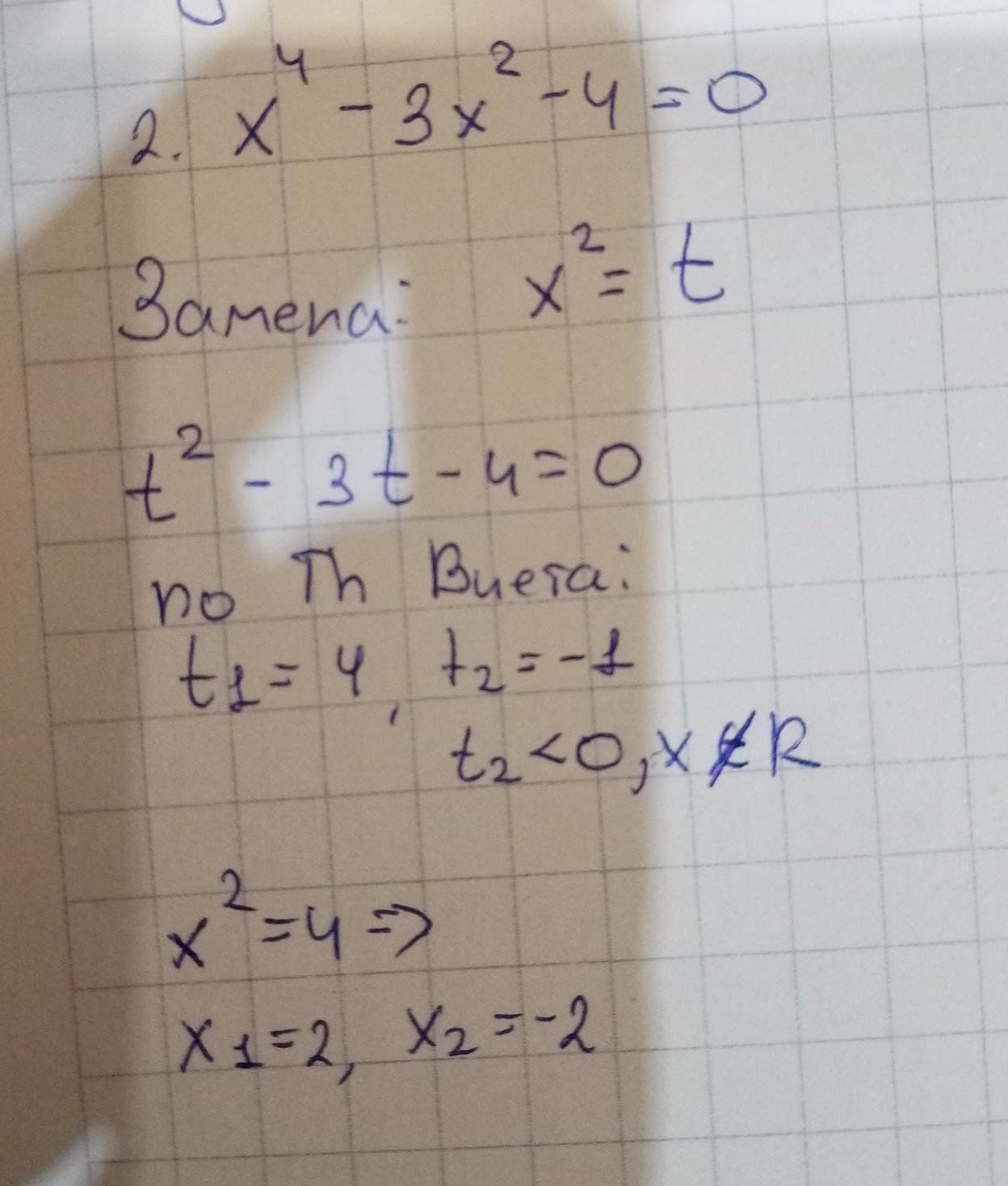
Автор ответа:
0
Задача:
Пусть x (см) - ширина, тогда (x + 4) (см) - длина. Так как площадь прямоугольника находится по формуле , а площадь равна 96 см² (по условию), то составим и решим уравнение:
- не удовлетворяет условию задачи
(см) - ширина
(см) - длина
Ответ: 12 см; 8 см
Уравнение:
Используем метод замены переменной.
Пусть x² = a, тогда:
Подставляем вместо x² = a получившиеся корни:
- нет корней
Ответ: 2; -2
Похожие вопросы
Предмет: Английский язык,
автор: samojlove
Предмет: Другие предметы,
автор: t031976
Предмет: Русский язык,
автор: MaxSa
Предмет: Математика,
автор: эля614
Предмет: Алгебра,
автор: олег501