Предмет: Алгебра,
автор: Anastacia16
Диференціальні рівняння.
Вища математика
Приложения:
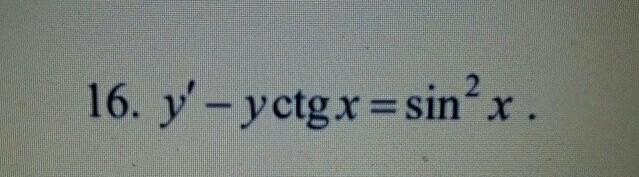
Ответы
Автор ответа:
1
Інтегруємо обидві частини диференціального рівняння
Отримали загальний розв'язок диф. рівняння
Похожие вопросы
Предмет: Другие предметы,
автор: БарбариSка
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: маоло
Предмет: История,
автор: yusi1234
Предмет: Математика,
автор: Инав