Предмет: Алгебра,
автор: ASV260
помогите решить!!!!!!
Приложения:
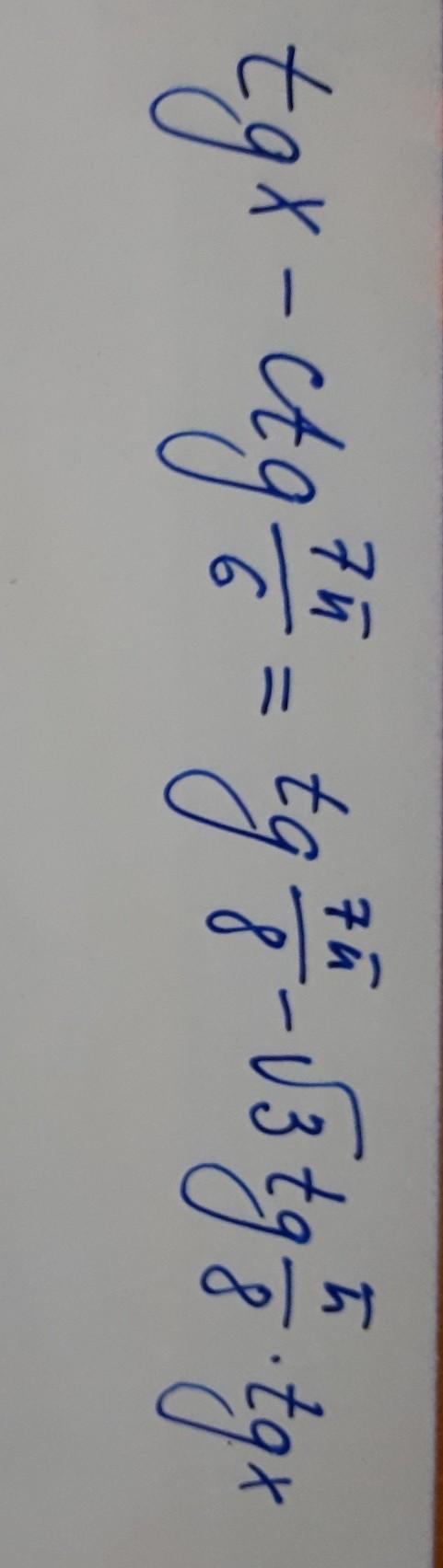
Ответы
Автор ответа:
1
P.S. В условии в левой части скорее всего знак (+), а не (-), т.к. с (-) формулы tg(a-b) или tg(a+b) не будет получаться.
NNNLLL54:
в принципе в условии можно написать и наоборот: в левой части оставить знак (-), а в правой части перед 2-ым слагаемым оставить (+). Тогда будет tg(a+b).
Похожие вопросы
Предмет: Русский язык,
автор: ШЕХИРЕВА1
Предмет: Русский язык,
автор: elfxf
Предмет: Английский язык,
автор: chetkij
Предмет: Математика,
автор: 4564mamed
Предмет: Алгебра,
автор: svetlanak71