Помогите мне решить две задачи срочно надо!!! Задачи на фотке
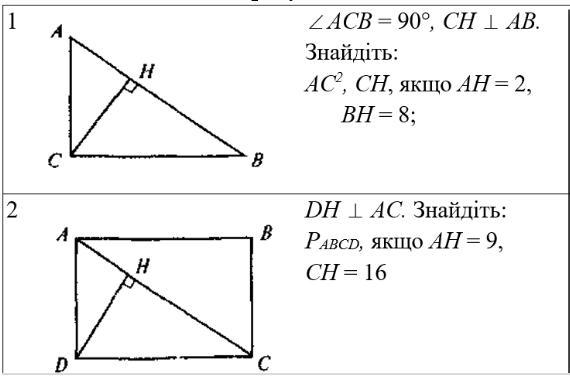
Ответы
Ответ:
1) 20 2) 70
Объяснение:
1. Для решения будем использовать только теорему Пифагора:
1) ΔАВС:
AC² + BC² = AB²
BC² = AB² - AC²
2) ΔAHC:
AH² + CH² = AC²
CH² = AC² - AH²
3) ΔHBC:
CH² + BH² = BC²
CH² = BC² - BH²
4) Из действия 2 и действия 3 составим уравнения:
CH² = AC² - AH² и CH² = BC² - BH², а значит:
AC² - AH² = BC² - BH²
5) Из действия 1 известно, что BC² = AB² - AC², а значит:
AC² - AH² = (AB² - AC²) - BH²
Перенесём AC² из правой части в левую, а AH² из левой части в правую:
AC² - AH² = AB² - AC² - BH²
AC² + AC² = AB² - BH² + AH²
2AC² = AB² - BH² + AH²
AC² = (AB² - BH² + AH²) ÷ 2
6) AB = AH + BH = 2 + 8 = 10
Решим уравнение:
AC² = (AB² - BH² + AH²) ÷ 2
AC² = (10² - 8² + 2²) ÷ 2
AC² = (100 - 64 + 4) ÷ 2
AC² = 40 ÷ 2
AC² = 20
Ответ: AC² = 20
2. Здесь тоже будем использовать теорему Пифагора:
1) ΔACD:
AD² + CD² = AC²
AD² = AC² - CD²
2) ΔAHD:
AH² + HD² = AD²
HD² = AD² - AH²
3) ΔHCD:
HD² + HC² = CD²
HD² = CD² - HC²
4) Из действия 2 и действия 3 составим уравнения:
HD² = AD² - AH² и HD² = CD² - HC², а значит:
AD² - AH² = CD² - HC²
5) Из действия 1 известно, что AD² = AC² - CD², а значит:
AC² - CD² - AH² = CD² - HC²
Перенесём HC² из правой части в левую, а CD² из левой части в правую:
AC² - AH² + HC² = CD² + CD²
AC² - AH² + HC² = 2CD²
CD² = (AC² - AH² + HC²) ÷ 2
6) AC = AH + HC = 9 + 16 = 25
Решим уравнение:
CD² = (AC² - AH² + HC²) ÷ 2
CD² = (25² - 9² + 16²) ÷ 2
CD² = (625 - 81 + 256) ÷ 2
CD² = 400
CD = √400 = 20
7) Из действия 1 известно, что AD² = AC² - CD², а значит:
AD² = 25² - 400
AD² = 625 - 400
AD² = 225
AD = √225 = 15
8) AD = BC, a CD = AB поскольку ABCD - это прямоугольник. Значит:
Периметр ABCD = AB + BC + CD + AD
P ABCD = 20 + 15 + 20 + 15 = 70
Ответ: P ABCD = 70