Question

ПОМОГИТЕ ПОЖАЛУЙСТА!!! ОТДАЮ ВСЕ СВОИ БАЛЫ

Answer 1

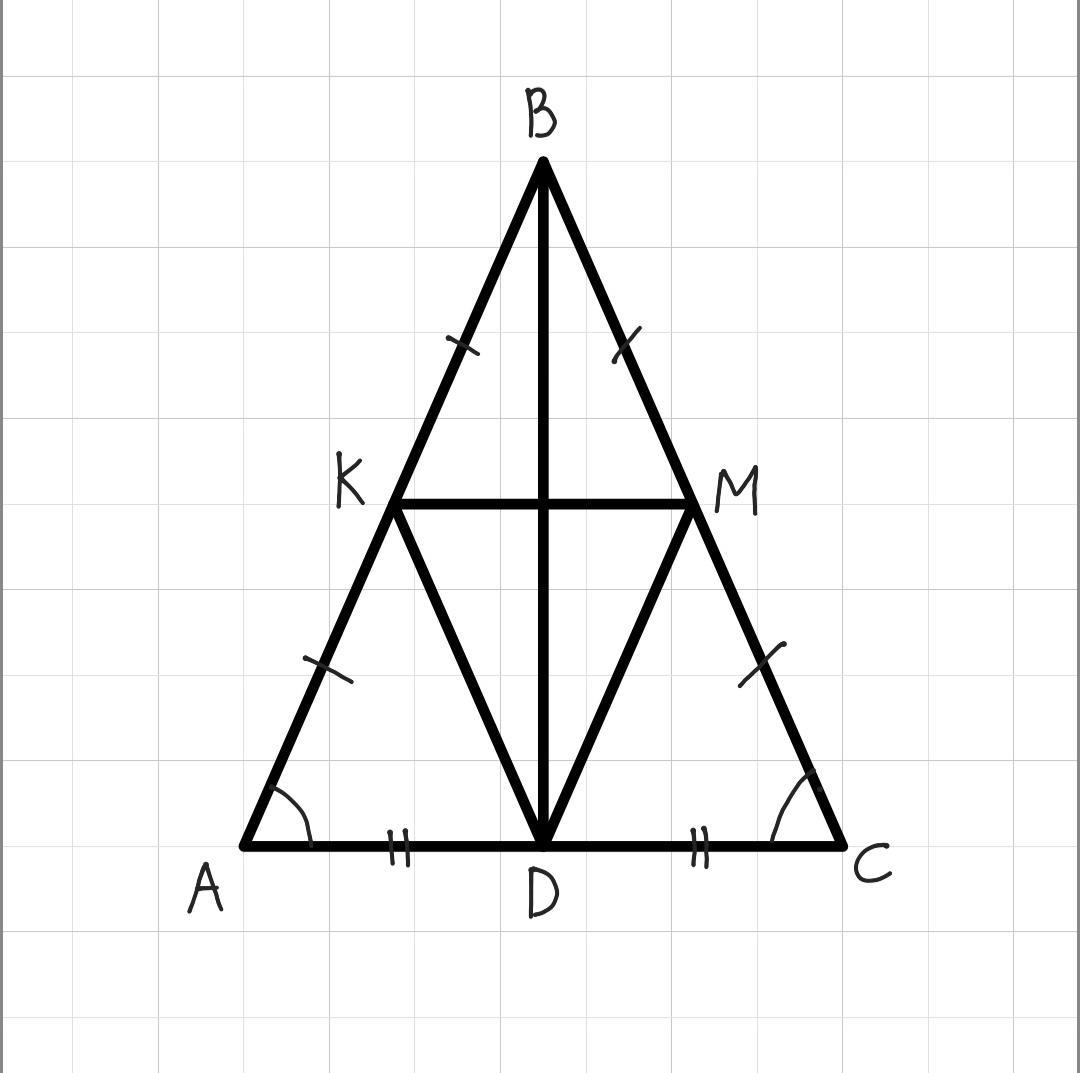
Дано: ΔABC - рівнобедрений, АВ=ВС, BD - медіана, К ∈ АВ, М ∈ ВС, АК=КВ, МС=МВ.

Довести: ΔAKD=ΔCMD.

Доведення.

Оскільки АВ=ВС, К і М - середини цих сторін (АК=КВ, МС=МВ), то АК=КВ=МС=МВ.

Оскільки BD - медіана ΔАВС за умовою, то вона ділить основу АС на рівні відрізки: AD=DC.

ΔАВС - рівнобедрений => кути при основі рівноб. трикутника рівні => ∠А=∠С.

Розглянемо ΔAKD і ΔCMD:

AK=MC;

∠A=∠C;

AD=DC.

Отже, трикутники AKD і CMD рівні за двома сторонами і кутом між ними (І ОРТ), що і т.б.д.