Question

уравнения 10-11 кл
помогите пожалуйста ​

Answer 1

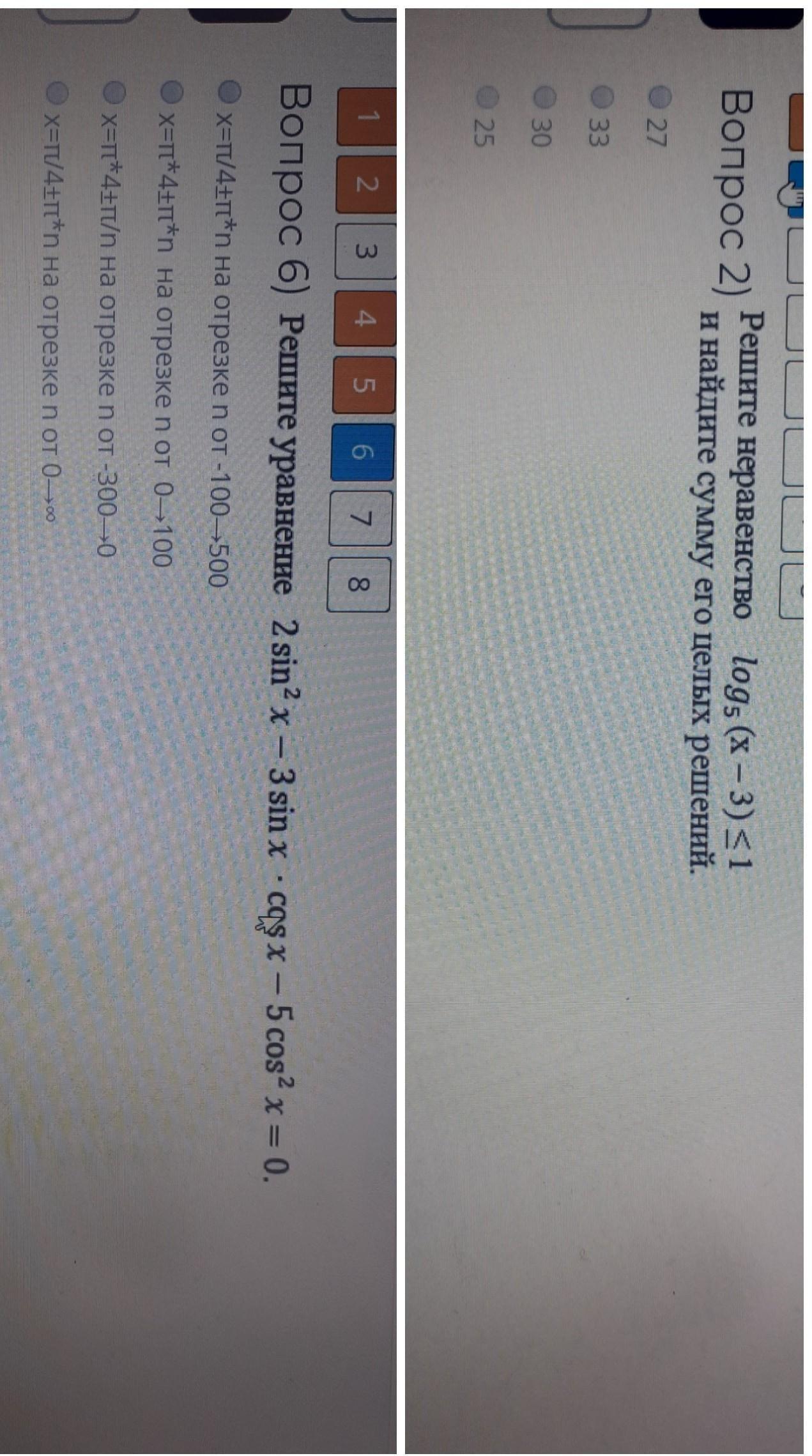
Вопрос № 2.

Начинаем такое добро, конечно же, с ОДЗ:

x - 3 > 0

x > 3

Теперь, со спокойной совестью можно приступить к уравнению:

  $log_{5}({x-3})\leq 1\\log_{5}({x-3})\leq log_{5}5\\x-3\leq 5\\x\leq 8$

Подставляя в ОДЗ получим следующий промежуток:

( 3 ; 8]

Найдем сумму целых чисел, удовлетворяющих промежутку:

4 + 5 + 6 + 7 + 8 = 30

Ответ: 30

Вопрос № 6

2sin²x - 3sinx * cosx - 5cos²x = 0

Итак. Перед тем, как решить данной уравнение, хотелось бы напомнить, что тангенс, это не только отношений противолежащего катета к прилежащему, а также отношение sin к cos. Тогда, все что нам нужно - разделить уравнение на cos²x:

2tg²x - 3tgx - 5 = 0

_____________________

P.S делить можно было и на sin²x. Это не принципиально. Тогда мы бы перешли не к тангенсу, а к котангенсу. На ваш вкус)

_____________________

Предлагаю ввести замену для решения данного уравнения.

Пусть tgx = t. Тогда:

2t² - 3t - 5 = 0

D = b² - 4ac = 9 - 4 * 2 * (-5) = 49

t(1) = (-b-√D)/2a = - 1

t(2) = (-b+√D)/2a = 5/2

Вернемся к замене:

tgx = -1    ⇒    x = 3п/4 + Пn n ∈ z

tgx = 5/2     ⇒    x = arctg (5/2) + Пn n ∈ z

Ответ: 3п/4 + Пn n ∈ z и arctg (5/2) + Пn n ∈ z