Question

Решите 4х^3 - 25x меньше 0

Answer 1

$4x^{3} - 25x < 0$

ОДЗ: $x \in R$

$x(4x^{2} - 25) < 0$

Найдем точки пересечения с осью абсцисс:

$x(4x^{2} - 25) = 0$

$\left[\begin{array}{ccc}x = 0 \ \ \ \ \ \ \ \ \ \\4x^{2} - 25 = 0\\\end{array}\right$

$\left[\begin{array}{ccc}x = 0 \ \ \ \ \\4x^{2} = 25\\\end{array}\right$

$\left[\begin{array}{ccc}x = 0 \ \ \ \ \\x^{2} = \dfrac{25}{4} \\\end{array}\right$

$\left[\begin{array}{ccc}x = 0 \ \ \ \\x = \pm \dfrac{5}{2} \\\end{array}\right$

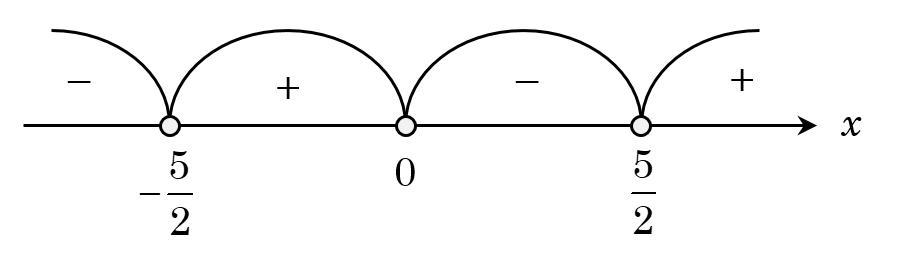
Нарисуем координатную прямую и отметим на ней точки пересечения с осью абсцисс, и найдем значение функции $y = 4x^{3} - 25x$ на каждом участке ("+" — если функция находится над осью абсцисс, "-" — если функция находится под осью абсцисс), подставляя в функцию число из промежутка (см. вложение).

Так как у нас неравенство $y < 0$, то нас устроят промежутки со знаком "-", не включая точки пересечения с осью абсцисс.

Ответ: $x \in \left(-\infty ; -\dfrac{5}{2} \right) \cup \left(0; \ \dfrac{5}{2} \right)$