Предмет: Алгебра,
автор: federikorus
9 класс. Преобразуйте, чтобы было можно построить график. Не получается ничего толкового...
Приложения:
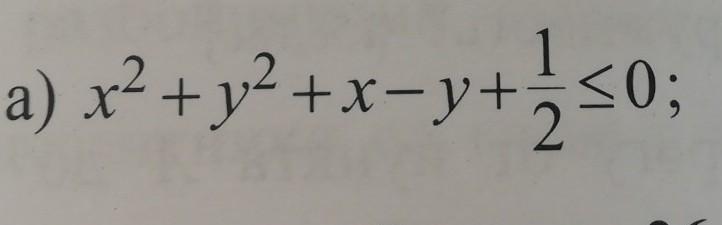
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Получаем слева уравнение окружности с центром в точке
Заметим, что полученное неравенство выполняется, тогда и только тогда, когда , так как сумма квадратов не может быть отрицательной. Получаем, что
- решение.
federikorus:
Спасибо. Странно, что такой лёгкий номер не решил. Зарешался)
Красивое решение.
Похожие вопросы
Предмет: Русский язык,
автор: mixgirl
Предмет: Русский язык,
автор: dana2004
Предмет: Русский язык,
автор: akulin
Предмет: Алгебра,
автор: RazPid
Предмет: Алгебра,
автор: щ76з6з6з6з6з6з