Предмет: Математика,
автор: valeriakatkina
Номер 22.13. Расписать каждую, пожалуйста!!!
Приложения:
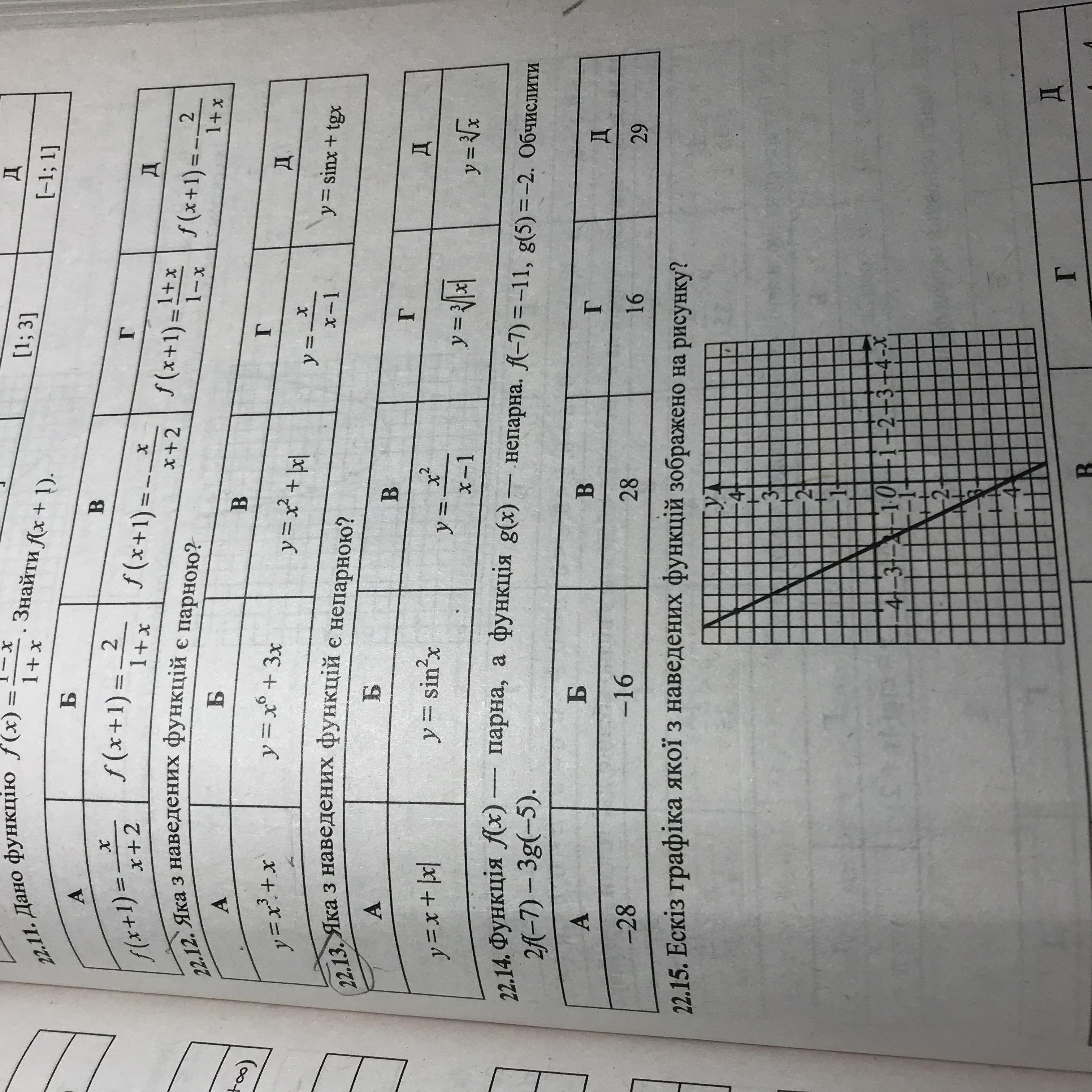
Ответы
Автор ответа:
0
Ответ:
Д
Пошаговое объяснение:
Необхідна умова непарності - симетричність відносно області визначення функції. Достатня умова непарності:
.
A:
Отже, функція ні парна, ні непарна.
Б:
Враховуючи непарність синусоїди, маємо, що при піднесенні мінус зникає і тому функція парна.
В:
Це дає право сказати, що ця функція ні парна, ні непарна.
Г:
Модуль - парна функція, отже мінус під кубічним коренем зникне і функція є парною.
Д:
.
Так як необхідна й достатня умови виконуються, то функція непарна.
Похожие вопросы
Предмет: Русский язык,
автор: vbkf2098
Предмет: Английский язык,
автор: k2001joir
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: OulianaMiMiMi