Предмет: Геометрия,
автор: artemvorinin
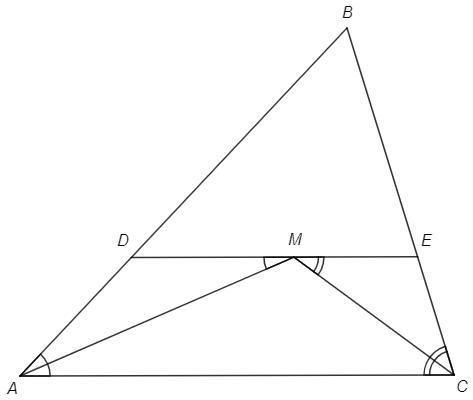
Внутри ABC выбирается точка m. через него проводится прямая линия, параллельная стороне AU и пересекающая стороны AB и BC соответственно в точках E, MD= AD и ME= EC. Докажите, что M-точка пересечения бисектрического треугольника.
Ответы
Автор ответа:
1
∠DAM=∠DMA (AD=DM, △ADM - равнобедренный)
∠CAM=∠DMA (накрест лежащие при DE||AC)
∠DAM=∠CAM, AM - биссектриса
Аналогично CM - биссектриса
Биссектрисы треугольника пересекаются в одной точке.
M - точка пересечения биссектрис.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sdfrtyukhgfdvgk
Предмет: Русский язык,
автор: poma123456
Предмет: Русский язык,
автор: happylera
Предмет: Обществознание,
автор: POMOZaka
Предмет: Математика,
автор: N3BECTHOCTb